Python と OpenCV でデッサンスケールを作る

　今回は小物ネタです。

• 2020/10/22 更新: アルファブレンドを実装し、グリッド線の不透明度を設定できるようになりました。

概要

　以下のような、デッサンスケールと呼ばれる道具をご存知でしょうか。

出典: はかり棒・デッサンスケール - はかりぼう・でっさんすけーる | 武蔵野美術大学 造形ファイル

　実物の観察に基づく素描の際に、構図を検討したり、全体的な比率を把握するために用いられる道具です。詳しくは出典元URLの記事を読んでいただければと思います。

　このデッサンスケールは、本来的には実物にかざして使うものですが、デッサンスケールを用いて行われる「まず画面をグリッドに区切り、大まかな比率を把握する」という作業は、写真や絵の模写練習についても有用であると考えられます。また、現状、クリスタ や Procreate など一般に利用可能なお絵かきツールには、ガイドとして任意のグリッドを表示できる機能が備わっています。しかし、いずれのツールを用いても、「お手本の画像と同サイズのキャンバスがあり、両者に同じグリッドが引かれている」という状態にするのはやや手間がかかります。

　そこで今回は次のようなプログラムを作成しました。それは、以下のようなお手本画像が与えられたとき、

入力例

「その隣に同サイズの空白領域（以下『キャンバス』）を持ち、同様のグリッドが引かれた新たな画像」を出力するというものです。

出力例

この画像をお絵描きソフトで上のレイヤーに配置することで、グリッドを参考にしながら練習を行うことができます。

実装

コードは以下の通りです。

import cv2
import numpy as np
import argparse
import os


def get_args():
    parser = argparse.ArgumentParser()
    parser.add_argument('path', type=str)
    parser.add_argument('--dst_dir', type=str, default='./')
    parser.add_argument('--div', type=int, default=4)
    parser.add_argument('--alpha', type=float, default=0.2)
    parser.add_argument('--side', type=str, default='left')
    parser.add_argument('--prefix', type=str, default='')
    parser.add_argument('--postfix', type=str, default='_dessin_scale')
    args = parser.parse_args()
    return args


def imread_bgra(args):
    img = cv2.imread(args.path, flags=cv2.IMREAD_UNCHANGED)
    h, w, c = img.shape
    if c == 3:
        alpha = np.ones((h, w, 1), dtype='uint8') * 255
        img = np.dstack((img, alpha))
    return img


def draw_grid(img, canvas, args):
    h, w, c = img.shape
    alpha_uint8 = round(255 * args.alpha)

    for i in range(args.div - 1):
        # 2の倍数で分割する際, グリッド線に強弱をつける
        lw = (i % 2 + 1) if args.div % 2 == 0 else 1
        # draw horizontal line
        y_i = round((i + 1) * h / args.div)
        s_h = (0, y_i)
        t_h = (w, y_i)
        cv2.line(canvas, s_h, t_h, (0, 0, 255, alpha_uint8), lw)
        # draw vertical line
        x_i = round((i + 1) * w / args.div)
        s_v = (x_i, 0)
        t_v = (x_i, h)
        cv2.line(canvas, s_v, t_v, (0, 0, 255, alpha_uint8), lw)

    c_alpha = canvas[..., 3][..., np.newaxis] / 255.
    img = canvas * c_alpha + img * (1 - c_alpha)
    return img, canvas


def concat_canvas(img, canvas, args):
    if args.side == 'left':
        res = np.hstack((canvas, img))
    elif args.side == 'right':
        res = np.hstack((img, canvas))
    elif args.side == 'above':
        res = np.vstack((canvas, img))
    elif args.side == 'below':
        res = np.vstack((img, canvas))
    else:
        raise NotImplementedError
    return res


def save(res, args):
    try:
        os.makedirs(args.dst_dir)
    except OSError:
        pass
    res_name = f'{args.prefix}{os.path.basename(args.path)}{args.postfix}.png'
    cv2.imwrite(os.path.join(args.dst_dir, res_name), res)


def main(args):
    img = imread_bgra(args)
    canvas = np.zeros_like(img)
    img, canvas = draw_grid(img, canvas, args)
    res = concat_canvas(img, canvas, args)
    save(res, args)


if __name__ == "__main__":
    args = get_args()
    main(args)

プログラムが受け取る引数は次の通りです。

• path : 入力する画像へのパス。
• --dst_dir : 結果の画像を出力するディレクトリ。デフォルトは ./ なので、プログラムが存在する場所にそのまま吐き出す。
• --div : 画像を何分割するか。デフォルトは 4 。
• --side : お手本画像のどちら側にキャンバスを配置するか。デフォルトは leftなので、左側に置かれる（私が左利きなのでこうしています）。
• --alpha : グリッド線の不透明度。デフォルトは 0.5。
• --prefix : 出力画像名の先頭に付ける文字列。デフォルトはなし。
• --postfix : 出力画像名の末尾に付ける文字列。デフォルトは_dessin_scale となっており、NAME_dessin_scale.png のような画像が出力される。

実行例は次の通り。

$ python main.py images/ref.png --dst_dir=result/ --div=6

まとめ

　デッサンスケールの発想で、絵の模写練習用の画像を作成するプログラムを書きました。改善案としては、画像の分割数を縦横それぞれ指定できるようにするとか、グリッドの色指定まわりとかでしょうか。あるいは、ドラッグ&ドロップで生成できるようにするとか、グリッドを別画像に出したりもしたい気もしました。

Pytorch Lightning で生成モデル — Autoencoder

　最近は主に画像の深層生成モデルに取り組んでいます。ライブラリとしてはしばらくは PyTorch を使っていたのですが、最近、 構造的に書くことのできるラッパーとして Pytorch Lightning を使い始めました。

　今回、練習としてオートエンコーダを実装し、手書き数字データセットである MNIST およびその変種を用いて簡単な実験を行ったので、記事にまとめます。

Autoencoder は次元の圧縮と復元を行う

　オートエンコーダは、次元圧縮を行うエンコーダと、次元復元を行うデコーダのペアからなる生成モデルです。

　上図のように、「データセットの元をエンコーダに通して低次元空間で表現したのち、そのままデコーダに通して元の次元に復元した際、できるだけもとのデータを再現できるようにする」という方式で学習が行われます。ここで、データ空間より次元の小さい圧縮先の空間を潜在空間と称しています。

　今回は最も単純な例として、いくつかの 全結合層+活性化関数 のみからなるオートエンコーダを用います。また、潜在空間の次元は図示のために 2 次元としておきます。

Pytorch Lightning で整ったコードを書く

　PyTorch Lightning は、PyTorch コードを構造化するためのライブラリです。通常の PyTorch では、学習を行うモデルのクラスは nn.Module を継承しますが、 Lightning では、nn.Module を継承している pl.LighningModule を継承し、configure_optimizer および training_step メソッドを書きます。

以下２つのコードブロックは公式ドキュメントの例です。

import pytorch_lightning as pl
from pytorch_lightning.metrics.functional import accuracy

class LitModel(pl.LightningModule):

    def __init__(self):
        super().__init__()
        self.l1 = torch.nn.Linear(28 * 28, 10)

    def forward(self, x):
        return torch.relu(self.l1(x.view(x.size(0), -1)))

    def training_step(self, batch, batch_idx):
        x, y = batch
        y_hat = self(x)
        loss = F.cross_entropy(y_hat, y)
        return loss

    def configure_optimizers(self):
        return torch.optim.Adam(self.parameters(), lr=0.0005)

　通常の PyTorch での学習では、エポック単位およびバッチ単位で for ループを回していました。 training_step メソッドは、そうしたループの内側の処理に相当するメソッドであり、各バッチを受け取って損失を返します。Lightning では、for ループを回す部分をクラスにまかせることができるため、訓練を実行する部分は以下のように非常に簡単になります。

# dataloader
dataset = MNIST(os.getcwd(), download=True, transform=transforms.ToTensor())
train_loader = DataLoader(dataset)

# init model
model = LitModel()

# most basic trainer, uses good defaults
trainer = pl.Trainer()
trainer.fit(model, train_loader)

　その他、GPU を利用する際は Trainer のコンストラクタに使用する GPU 数を与えるだけでよく、GPUにデータを移すコードを書く必要がなくなります。また、並列化の際に、データセットのダウンロード処理が一度かつ一度だけ行われることを保証したりなど、細かなところで色々と面倒を見てくれます。pl.LightningModule は nn.Module を継承しており、機能的に上位互換であるため、 nn.Module で使えるメソッドはすべて nn.Module に期待する通りに使えます。

　類似のラッパーとしては、catalyst, fastai, ignite などがあります。私は他を実際に試したわけではないので、比較については以下の記事などが参考になるかと思います。

PyTorch 三国志（Ignite・Catalyst・Lightning） - Qiita

　今回、2020年8月10日現在で stable には未実装な pl.DataModule を使用するため 、バージョンは 0.9.0rc2 を使用しました。

pip install pytorch-lightning==0.9.0rc2

Lightning はまだ破壊的変更も多く、過去の記事のコードをコピペしてもそのままでは動かないことが多いです。設計思想が大幅に変わるわけではないにせよ、バージョンの合った公式ドキュメントを確認することをおすすめします。

実装

モデル本体

　import なども含めたコードの全容は github

https://github.com/optie-f/PL_AutoEncoder

を見てもらうとして、主な部分を解説します。

　まず、線形層と活性化関数からなるモジュールを作ります。

class LAN(nn.Module):
    """
    Linear-Activation-Normalization.
    """

    def __init__(self, in_dim, out_dim, activation=nn.ReLU(True), norm=nn.Identity()):
        super(LAN, self).__init__()
        self.L = nn.Linear(in_dim, out_dim)
        self.A = activation
        self.N = norm

    def forward(self, x):
        z = self.L(x)
        z = self.A(z)
        z = self.N(z)
        return z

一応 BatchNormalization などを配置できるようにもしておきましたが、今回は使用しません。

　次に、エンコーダおよびデコーダとなるモジュールです。

class DENcoder(nn.Module):
    def __init__(self, dimentions, mid_activation, last_activation):
        super(DENcoder, self).__init__()
        layers = []
        in_dims = dimentions[:-1]

        for i, in_dim in enumerate(in_dims):
            activation = last_activation if i + 1 == len(in_dims) else mid_activation
            out_dim = dimentions[i + 1]
            layers.append(
                LAN(in_dim, out_dim, activation=activation)
            )

        self.model = nn.Sequential(*layers)

    def forward(self, x):
        return self.model(x)

encoder でも decoder でも使うので DENcoder です。他の名称は思いつきませんでした。コンストラクタでは、dimentionsとして「入力データの次元および各層の出力の次元」の一次元整数配列、mid_activation として中間層の（最終出力以外の）活性化関数、last_activation として最終出力への活性化関数をそれぞれ渡して、インスタンスを作成します。

　なぜ各層を直接書かないか。全結合層を積んでいくときには、 [Linear(d1, d2), Linear(d2, d3), ...] というように、各層の入力次元を前の層の出力次元と揃える必要があります。これを直接書くのではなく、[d1, d2, d3, ... ] という配列を渡して作ることで、より指定しやすく、また、深さや幅を調整しやすくするという意図でこのような実装にしています。

　次に、全体のモデルです。ここで pl.LightningModule が登場します。以下で各メソッドについて説明します。

class AutoEncoder(pl.LightningModule):
    def __init__(self, in_dimentions):
        super(AutoEncoder, self).__init__()
        out_dimentions = list(reversed(in_dimentions))
        self.encoder = DENcoder(in_dimentions, nn.ReLU(True), nn.Identity())
        self.decoder = DENcoder(out_dimentions, nn.ReLU(True), nn.Tanh())
        self.criterion = nn.MSELoss()

    def forward(self, img):
        x = img.view(img.size(0), -1)
        z = self.encoder(x)
        x_hat = self.decoder(z)
        img_recon = x_hat.view(img.size())
        return img_recon

    def training_step(self, batch, batch_idx):
        img, _ = batch
        img_recon = self.forward(img)
        loss = self.criterion(img, img_recon)

        if self.global_step % self.trainer.row_log_interval == 0:
            sqrt_nb = int(sqrt(img.size(0)))
            self.logger.experiment.add_image(
                "image/original",
                make_grid(img, sqrt_nb, normalize=True, range=(-1, 1)),
                self.global_step
            )
            self.logger.experiment.add_image(
                "image/reconstructed",
                make_grid(img_recon, sqrt_nb, normalize=True, range=(-1, 1)),
                self.global_step
            )

        return {'loss': loss, 'log': {'loss': loss}}

    def configure_optimizers(self):
        optimizer = optim.Adam(self.parameters(), lr=1e-3, weight_decay=1e-5)
        return optimizer

　コンストラクタについて。ここでは、エンコーダとデコーダの幅と深さは対称にしているため、コンストラクタでは in_dimentions 引数としてエンコーダ用の配列のみを受け取り、デコーダはこれを反転させることで作っています。また、損失関数を self.criterion に代入しており、今回は平均自乗誤差です。

　forward メソッドについて。このモデルへ入力されるのは (batchsize, C, H, W) という形状の画像ですが、全結合層への入力では一次元にする必要があるので、 (batchsize, CxHxW) というベクトルの形に変形し、出力時に再び画像の形に戻す処理を行っています。

　training_step メソッドについて。前述の通り、訓練ループの内側に相当する関数で、batch および batch の添字を受け取り、損失を返します。

　Lightning では、Trainer のコンストラクタの引数に logger （後述）を渡すことで、 Tensorboard などを用いて学習のリアルタイム計測監視を行うことができます。これに関係する処理もtraining_step に書きます。例えば上記のコードのように、返り値を dict にした上で、'log': {'loss': loss,...} のような要素を追加することで、損失関数など指定したスカラー値の訓練中の変動がプロットされます。

　スカラーのプロットのほか、画像などを表示する場合は明示的にメソッドを呼び出す必要があるようです。ここでは、訓練における現在のステップ数が記録されている self.global_step および、 Trainer のコンストラクタに渡す self.trainer.row_log_interval から、「特定のステップ数のときに、元画像と復元画像を並べて表示する」という処理を書いています。

DataModule

　ここで、pl.LightningDataModule というものを用意しておきます。これは、train,validation,test 用のdataset および Dataloader を統一的に管理するものであり、trainer.fit() あるいは trainer.test() に渡すことで、訓練時・バリデーション時・テスト時のデータセットの読み分けを行います。

dataset_classes = {
    'MNIST': MNIST,
    'KMNIST': KMNIST,
    'FashionMNIST': FashionMNIST,
    'CIFAR10': CIFAR10
}

class NormalizeAllChannel():
    """
    a normalization transform using given mean & std
    but accepts any number of channels.
    By default, [0, 1] -> [-1, 1]
    """

    def __init__(self, mean=0.5, std=0.5):
        self.mean = 0.5
        self.std = 0.5

    def __call__(self, x):
        return (x - self.mean) / self.std

class DataModule(pl.LightningDataModule):
    def __init__(self, data_dir='./data', data_name='', batchsize=32):
        super().__init__()
        self.data_dir = data_dir
        self.batch_size = batchsize
        self.transform = transforms.Compose([
            transforms.ToTensor(),
            NormalizeAllChannel()
        ])
        if data_name in dataset_classes:
            self.Dataset = dataset_classes[data_name]
        else:
            raise NotImplementedError

    def prepare_data(self):
        self.Dataset(self.data_dir, download=True)

    def setup(self, stage=None):
        if stage == 'fit' or stage is None:
            self.dataset = self.Dataset(
                self.data_dir,
                train=True,
                transform=self.transform
            )
            size = len(self.dataset)
            t, v = (int(size * 0.9), int(size * 0.1))
            t += (t + v != size)
            self.dataset_train, self.dataset_val = random_split(self.dataset, [t, v])

        if stage == 'test' or stage is None:
            self.dataset_test = self.Dataset(
                self.data_dir,
                train=False,
                transform=self.transform
            )

    def train_dataloader(self):
        return DataLoader(
            self.dataset_train,
            batch_size=self.batch_size,
        )

    def val_dataloader(self):
        return DataLoader(
            self.dataset_val,
            batch_size=self.batch_size,
        )

    def test_dataloader(self):
        return DataLoader(
            self.dataset_test,
            batch_size=self.batch_size,
        )

必須なメソッドは prepare_data, setup,train_dataloader の 3 つです。今回は、データセットとして MNIST, KMNIST, FashionMNIST, CIFAR10 のみを扱う予定なので、コンストラクタの引数で文字列で data_name を受け取り、これに応じて Dataset クラスを保持しておきます（インスタンスではなく、クラスそのものです）。

　まず prepare_data が呼ばれます。ここでデータのダウンロード処理を行うことが想定されているようです。ここに書いておくことで、並列化した際にもうまくやってくれるようです。

次に setup が呼ばれます。このとき、呼ばれたのが trainer.fit() か trainer.test() かに応じて、stage 引数に 'fit' か 'test' かが渡されるので、これに応じて dataset オブジェクトを準備しておきます。

　train_dataloader はそのあとに呼ばれるようです。DataLoader オブジェクトを返します。

訓練

訓練用のコードは以下です。上から順番に見ていきます。

def train(hparams):
    train_loader = DataModule(data_name=hparams.dataset_name)
    train_loader.prepare_data()
    train_loader.setup()

    in_dim = np.prod(train_loader.dataset[0][0].size())
    dimentions = [in_dim, 512, 128, 64, 12, 2]

    autoEncoder = AutoEncoder(dimentions)
    print(autoEncoder)

    checkpoint_callback = ModelCheckpoint(
        save_top_k=1,
        verbose=True,
        monitor='loss',
        mode='min',
        prefix=''
    )

    logger = TensorBoardLogger('log', name=hparams.dataset_name)
    trainer = Trainer(
        logger=logger,
        default_root_dir='./log',
        checkpoint_callback=checkpoint_callback,
        row_log_interval=50,
        max_epochs=hparams.max_epochs,
        gpus=hparams.gpus,
        tpu_cores=hparams.tpu_cores
    )

    trainer.fit(autoEncoder, train_loader)

def main():
    parser = ArgumentParser()
    parser.add_argument('--gpus', default=None)
    parser.add_argument('--tpu_cores', default=None)
    parser.add_argument('--max_epochs', default=50)
    parser.add_argument('--dataset_name', default="MNIST")
    args = parser.parse_args()

    train(args)

if __name__ == "__main__":
    main()

　本来、train_loader.prepare_data() および train_loader.setup() を我々で呼ぶ必要はないですし、むしろおそらく呼ぶべきではないのですが、ここでは入力の次元をデータセットから計算する必要があるために初めに呼んでしまっています。ここはもっと良いやり方があるのかもしれません。

　ModelCheckpoint は学習しながらモデルを保存するためのコールバックを司るクラスで、インスタンスを Trainer のコンストラクタに渡して使います。loss などの指定した指標が最も少なくなった上位 k 件を保存する、などといった指定ができます。

　TensorBoardLogger は、Tensorboard オブジェクトの Lightning 向けラッパーで、こちらもインスタンスを Trainer に渡して使います。

　これらを Trainer のコンストラクタに渡すことでインスタンスを得ています。使用する GPU 数や TPU のコア数もここで指定します。

実験と可視化

MNISTの潜在空間

　学習および結果の確認は Google Colabolatory で行いました。以下のコードブロックはそのままノートブックのセルへの記述です。

　まず、リポジトリからクローンし、Lightning のインストールを行って作業ディレクトリを移動します。

!git clone https://github.com/optie-f/PL_AutoEncoder
!pip install pytorch-lightning==0.9.0rc2
%cd PL_AutoEncoder

　 学習しながら確認するため、あらかじめ Tensorboard を表示しておきます。

%load_ext tensorboard
%tensorboard --logdir log/

　その後、訓練を始めます。前述のコードにある通り、--dataset_name のデフォルト値は MNIST になっているので、MNIST に対する訓練が始まります。

!python train.py --gpus 1

　訓練が始まったあと、さきほど表示した Tensorboard を更新すると、リアルタイムで損失や復元画像を確認することができます。以下図は訓練終了後のものですが、左側がデータセットの画像、右側が復元された画像です。

ややぼやけており、最上段の「8」や「5」など怪しいものも散見されますが、概ね元の数字形状は視認できるといってよいでしょう。

　また、テストデータから 10000 件をエンコードし、2次元潜在空間における散布図を作成し、ラベル（実際に何の数であるか）ごとに色分けをすると、以下のようになりました。

なんとなく各数字ごとにまとまっていた位置に現れているような気はします。これだけではわかりにくいので、今度は逆に、潜在空間内で、$(0, 0)$ を中心とした $50 × 50$, 幅 1 のグリッドをとり、格子点をデコーダを通すことでどのような数字として現れるかを見ることにします。

例えば「8」と「2」が隣接した領域にあり、その間には「8」とも「2」ともつかないような数字が並んでいたりすることが観察されます。

　こうした潜在空間における分布は訓練をするたびに異なった現れ方をします。別の試行での潜在空間は以下のようなものでした。

様子は異なっていますが、概ね中心から放射状に広がっているように見えます。

潜在空間を移動する点を逐次復元することで、文字が変化するアニメーションなども作れそうなイメージはつきますね。

可視化に使用したコードは以下の通りです。

from modules.data_loader import DataModule
from modules.model import AutoEncoder
import numpy as np
import torch
import matplotlib.pyplot as plt
import seaborn as sns
import os


data_name = "MNIST"
testsize = 10000

# 画像（とラベルの読み込み）
dataModule = DataModule(data_name=data_name, batchsize=testsize)
dataModule.setup(stage="test")
test_loader = dataModule.test_dataloader()
images, labels = iter(test_loader).next()

# 最新バージョンの最新チェックポイントのパス
versions_dir = os.path.join('./log/', data_name)
versions = sorted(os.listdir(versions_dir))
ckpts_dir = os.path.join(versions_dir, versions[-1], 'checkpoints/')
ckpts = sorted(os.listdir(ckpts_dir))
ckpt_path = os.path.join(ckpts_dir, ckpts[-1])

# モデルの読み込み
dimentions = [np.prod(images[0].size()), 512, 128, 64, 12, 2]
autoEncoder = AutoEncoder(dimentions)
autoEncoder.load_state_dict(torch.load(ckpt_path)["state_dict"])
autoEncoder.freeze()

# テストデータの 10000 枚の画像が潜在空間でどのように分布するかの可視化
z = autoEncoder.encoder(images.view(10000, -1))
np_z = z.to('cpu').detach().numpy().copy()
np_labels = labels.to('cpu').detach().numpy().copy()

sns.set()
plt.figure(figsize=(12, 10))
plt.scatter(np_z[:,0], np_z[:,1], c=np_labels, s=1)
plt.colorbar()
plt.show()

# 潜在空間での格子点を考える。その各点はどのような画像になるかの可視化
latent_grid = np.array([[(x+0.5), (y+0.5)] for x in range(-25,25) for y in range(-25,25)])
z_grid = torch.tensor(latent_grid, dtype=torch.float32)
recon = autoEncoder.decoder(z_grid)
np_recon = recon.view(50, 50, 28, 28).to('cpu').detach().numpy().copy()

sns.set(style='dark')
plt.figure(figsize=(20, 20))
plt.imshow(np_recon.swapaxes(1,2).reshape(28*50, 28*50), cmap='gray')
plt.show()

FashionMNIST, KMNIST, CIFAR10 でも試す

　今回はMNISTのほか、ファッション雑貨の低解像度写真？データセット FasionMNIST、崩し字データセットの KMNIST、カラー写真の CIFAR10 でも同様の実験を行っていました。以下に結果を載せます。

FasionMNIST

　ファッション雑貨データセットです。「MNISTは簡単すぎてベンチマークにもならない」という課題から作られたそうです。

復元の様子。

ストライプ模様のシャツなどは模様がぼやけてしまっていますが、種別は保持されていそうです。ただ左上のように暗めの色のズボンなどは何が何だか分からなくなっています。こうした点から、MNISTの数字認識からの難易度上昇を感じさせます。

潜在空間マップ。

長袖の上着とカバンが接する領域、長袖からワンピースへの遷移などが面白いですね。

KMNIST

　崩し字です。こちらは比較的最近のデータセットではなかったでしょうか。字種が多く、しかも各種類ごとに数が均等ではないそうで、認識問題としての難易度は跳ね上がりそうです。

復元の様子。

「つ」「ハ」「れ」は復元できているのはわかりますが、それらと形が近い字が「つ」「ハ」「れ」に吸収されてしまっている感じがあります。

潜在空間マップ。

左左下あたりが存在しない字になっている気がします。

CIFAR10

　一般物体認識に用いられる写真のデータセットです。MNIST が $28 \times 28 \times 1 = 784$ 次元であり、MNIST変種もその程度であったのに対して、CIFAR10 は $32 \times 32 \times 3 = 3072$ 次元あります。そもそも airplane, automobile, bird, cat, deer, dog, frog, horse, ship, truck というクラスの写真分類であり、一つのクラス内でもMNISTよりずっとバリエーションが豊かです。つまり、難しいです。

復元の様子。

マッピングをしたかったので潜在空間を2次元にすることにこだわっていたのですが、このようにまったく復元できていないので、限界がありそうです。

よくわからなかった点

前項の可視化コードで、モデルを読み込む際に以下のようにしていますが、

dimentions = [np.prod(images[0].size()), 512, 128, 64, 12, 2]
autoEncoder = AutoEncoder(dimentions)
autoEncoder.load_state_dict(torch.load(ckpt_path)["state_dict"])

これは本来、公式ドキュメントの例を見る限り、以下のように書くだけでよいはずです。

autoEncoder = AutoEncoder.load_from_checkpoint(ckpt_path)

しかし、これを実行すると、このようなエラーに遭遇します。

46     def __init__(self, in_dimentions):
     47         super(AutoEncoder, self).__init__()
---> 48         out_dimentions = list(reversed(in_dimentions))
     49         self.encoder = DENcoder(in_dimentions, nn.ReLU(True), nn.Identity())
     50         self.decoder = DENcoder(out_dimentions, nn.ReLU(True), nn.Tanh())

TypeError: 'dict' object is not reversible

これはバグということになるのでしょうか。追って Lightning のコードなどを確認できればしたいところです。

おわりに

PyTorch Lightning でオートエンコーダを実装しました。次があれば、今回のコードを拡張しながら変分オートエンコーダ（VAE）でも実装しようと思います。

制約つき最適化問題を解くための二乗罰則法と対数バリア法および Julia による実装

復習シリーズ2. 表題の内容について自分の理解でまとめます.

前回:

optie.hatenablog.com

制約つき最適化問題

とは, 以下のように定式化されるものです.

$\mathcal{X} \subset \mathbb{R}^d$ 上の微分可能な目的関数 $f:\mathcal{X}\mapsto\mathbb{R}$ の最小値を求めよ. $$ \min_{\boldsymbol{x}\in\mathcal{X}} f(\boldsymbol{x}) \ \ \ \mathrm{subject \ to} \ \ \ \vec{g}(\boldsymbol{x})=\boldsymbol{0}, \ \vec{h}(\boldsymbol{x})\leq \boldsymbol{0} $$ $$ \vec{g}(\boldsymbol{x}) = ( g_1(\boldsymbol{x}),\ldots,g_m(\boldsymbol{x}))^{\mathrm{T}}$$ $$ \vec{h}(\boldsymbol{x}) = ( h_1(\boldsymbol{x}),\ldots,h_n(\boldsymbol{x}))^{\mathrm{T}}$$

ベクトルについては, 変数・定数は太字表記・関数は矢印表記ということにします. (あまり一般的ではないと思いますが, 自分が学習中に関数のベクトルに混乱したことがあったので…）

"subject to…" は「…という制約条件を持つ」という意味で, ベクトルの等式・不等式は要素ごとであるものとします.

この定式化では, $\boldsymbol{x}$ について, $ m $ 個の等式と $n$ 個の不等式による制約条件がかかっているという意味になります. （$m=0$ または $n=0$ でもかまいませんが, $m=n=0$ だと制約なしになります）

ある $\boldsymbol{x}_0$ が全ての制約条件 $\vec{g}(\boldsymbol{x}_0)=\boldsymbol{0}, \ \vec{h}(\boldsymbol{x}_0)\leq \boldsymbol{0} $ を満たすとき, $\boldsymbol{x}_0$ を実行可能解 feasible solution と呼びます. 実行可能解の中から目的関数を最小にするものを探そうというわけです.

結論から言うと, 制約つき最適化問題は, 等式・不等式問わず, 制約なし最適化問題に変換することで解くことができます.

そのため, 以下では等式・不等式制約問題の性質について触れつつ, そのいずれにも利用できる 二乗罰則法 を紹介します *1 . また, 不等式制約問題については, 対数バリア法 も紹介します.

その後, 二乗罰則法および対数バリア法を Julia で実装し, 簡単な不等式制約つき最適化問題を解く例を示します.

等式制約問題

まずは等式制約つき最適化問題から.

$$ \min_{\boldsymbol{x}\in\mathcal{X}} f(\boldsymbol{x}) \ \ \ \mathrm{subject \ to} \ \ \ \vec{g}(\boldsymbol{x})=\boldsymbol{0}$$ $$ \vec{g}(\boldsymbol{x}) = ( g_1(\boldsymbol{x}),\ldots,g_m(\boldsymbol{x}))^{\mathrm{T}}$$

前述の通り, 二乗罰則法という手法が知られています. そのアルゴリズムは以下のようなものです.

各 $k$ について, 次の $\boldsymbol{x}_{k+1} $を,

$\boldsymbol{x}_{k}$を初期値とした以下の制約なし最適化問題の解 として選ぶ: $$ \boldsymbol{x}_{k+1} \leftarrow \underset{\boldsymbol{x} \in \mathcal{X}}{\mathrm{argmin}} \
\left\{ f(\boldsymbol{x}) + c_k ||\vec{g}(\boldsymbol{x})||^2 \right\} $$ $c_k$ は $k$ の増加に従って徐々に増やす: $$ 0 < c_1 < c_2 < \ldots $$

これは, $ \vec{g}(\boldsymbol{x})=\boldsymbol{0}$ という制約条件を, 「$ \vec{g}(\boldsymbol{x})=\boldsymbol{0}$ からできるだけ離れないようにする」と読み替えたものと言えるでしょう.

すなわち, 点 $\boldsymbol{x}$ と直線（あるいは超平面） $ \vec{g}(\boldsymbol{x})=\boldsymbol{0}$ からの距離に応じて増える罰則項 $ c_k ||\vec{g}(\boldsymbol{x})||^2$ を加味した $$ f(\boldsymbol{x}) + c_k ||\vec{g}(\boldsymbol{x})||^2 $$ を最小化するという制約なし最適化問題を解くということです.

ここで, 「$c_k$ は $k$ の増加に従って徐々に増やす」ことで, 始めは ほぼ$f(\boldsymbol{x})$単体での最小化のような挙動をしながら, 徐々に制約条件$ \vec{g}(\boldsymbol{x})=\boldsymbol{0}$ を満たすように$\boldsymbol{x}_{k} $ が移動していくことを狙うアルゴリズムだといえます.

$c_k$をいかに決め, いかに増加させるかが難しい点です.

不等式制約問題

二乗罰則法は, 不等式制約問題:

$$ \min_{\boldsymbol{x}\in\mathcal{X}} f(\boldsymbol{x}) \ \ \ \mathrm{subject \ to} \ \ \ \vec{h}(\boldsymbol{x})\leq\boldsymbol{0}$$ $$ \vec{h}(\boldsymbol{x}) = ( h_1(\boldsymbol{x}),\ldots,h_n(\boldsymbol{x}))^{\mathrm{T}}$$

でも適用できます. 等式制約問題と同じ発想で,

各 $k$ について, 次の $\boldsymbol{x}_{k+1} $を,

$\boldsymbol{x}_{k}$を初期値とした以下の制約なし最適化問題の解 として選ぶ: $$ \boldsymbol{x}_{k+1} \leftarrow \underset{\boldsymbol{x} \in \mathcal{X}}{\mathrm{argmin}} \
\left\{ f(\boldsymbol{x}) + c_k \max\left(0, \vec{h}(\boldsymbol{x})\right)^2 \right\} $$ $c_k$ は $k$ の増加に従って徐々に増やす: $$ 0 < c_1 < c_2 < \ldots $$ ただし, $\max\left(0, \vec{h}(\boldsymbol{x})\right)^2 = \displaystyle \displaystyle \sum_{i=1}^{n}\max\left(0, h_i (\boldsymbol{x})\right)^2 $ とする.

という形になります.

等式制約問題では, $ \vec{g}(\boldsymbol{x})<\boldsymbol{0}$ と $ \vec{g}(\boldsymbol{x})>\boldsymbol{0}$ の両方にペナルティを課す必要がありましたが, 今回は $ \vec{h}(\boldsymbol{x})\leq\boldsymbol{0}$ という条件であるため, $\vec{h}(\boldsymbol{x})<\boldsymbol{0}$ である分には何も問題がないので, $ \vec{g}(\boldsymbol{x})>\boldsymbol{0}$ 側にだけ罰則を課すために, 罰則項が $ \max \left( 0, \vec{h}(\boldsymbol{x}) \right)$ となるという違いが生じています.

このアルゴリズムでは, 途中の解 $\boldsymbol{x}_k$は一般に, 実行可能領域の外側にも来る（$ \vec{g}(\boldsymbol{x}_k)>\boldsymbol{0}$）ため, 外点法とも呼ばれます.

等式制約を厳密に満たすことはそもそも数値計算では困難 *2 なので, 等式制約問題では解が実行可能領域から少し外れていてもあまり問題にはならないと考えられますが, 不等式制約問題では, 「実行可能領域の内側に解があってくれないと困る」という要求はありえます.

そんなとき, 前述の 外点法 に対して 内点法 と呼ばれる, 「常に実行可能領域の内側に解が存在することを保証する」手法のひとつが 対数バリア法 で, 以下のようなアルゴリズムです.

各 $k$ について, 次の $\boldsymbol{x}_{k+1} $を,

$\boldsymbol{x}_{k}$を初期値とした以下の制約なし最適化問題の解 として選ぶ: $$ \boldsymbol{x}_{k+1} \leftarrow \underset{\boldsymbol{x} \in \mathcal{X}}{\mathrm{argmin}} \
\left\{ f(\boldsymbol{x}) - c_k \log\right(-\vec{h}(\boldsymbol{x})\left) \right\} $$ $c_k$ は $k$ の増加に従って徐々に減らす: $$ c_1 > c_2 > \ldots > 0 $$ ただし, $\log\left(-\vec{h}(\boldsymbol{x})\right) =\displaystyle \sum_{i=1}^{n}\log\left(-h_i(\boldsymbol{x})\right) $ とする.

二乗罰則法での罰則項が $- c_k \log\left(-\vec{h}(\boldsymbol{x})\right) $ に変わりました. 障壁項と呼ぶことにします.

実数の範囲では $\log(x)$ は $x\leq 0$ では定義されず, $\underset{x\to +0}{\lim} \log(x) \to -\infty$ であることは（ここまで読んできた方なら）周知かと思います.

これを踏まえると, 上の障壁項は,

「 実行可能領域の内側から境界に近づけば $$\underset{\vec{h}(\boldsymbol{x}) \to -0}{\lim} \left\{- c_k \log\left(-\vec{h}(\boldsymbol{x})\right) \right\} \to \infty$$ となり, 実行可能領域の境界上 $\boldsymbol{x}=\boldsymbol{0}$ および外側 $\boldsymbol{x}>\boldsymbol{0}$ では定義されない」

ようなものであることがわかります.

ここで, $\log(x)$ は $x=1$ で正負が入れ替わるので, $-\vec{h}(\boldsymbol{x})\geq \boldsymbol{1}$ のときはむしろ目的関数を減少させる項となってしまい, おかしくなるのでは？と思われるかもしれません.

ですが, $c_k$ は $k$ の増加に従って $ c_1 > c_2 > \ldots > 0 $ と減らしていくものであったことを思うと, $c_k$が $0$ に近づくとき, 障壁項は

となるので, 問題なさそうです.

実装

それでは, Julia の時間です.

using LinearAlgebra

今回, 例として以下の最適化問題を数値的に解きます.

$$ \min_{x,y \in \mathbb{R}} 3 x^2 + 2 y^2 \ \mathrm{subject \ to} \ \ x+y \geq 1 $$

解析解は $(x,y) = (0.4,0.6)$ です.

目的関数と制約条件の定義と, 今回はステップ幅一定の単純な勾配法を用いることにします *3 .

function f(x)
    3x[1]^2+2x[2]^2
end

function h(x)
    1-(x[1]+x[2])
end

function ∇(f,x)
    h = 0.0001
    return [( f(x+[h,0]) - f(x-[h,0]) ) / 2h, 
            ( f(x+[0,h]) - f(x-[0,h]) ) / 2h]
end


function GradientDescent(f, init_x, ε=0.05)
    x = init_x
    m = 0.1
    while norm( ε.*∇(f,x) ) > m
            x = x - ε.*∇(f,x)
    end
    return x
end

まずは二乗罰則法です.

function SquarePenalty(f,h)
    x = (rand(2).+1)*20
    c = 2    #initialize
    ε = 2  # cの増加率
    m = 0.001  # 収束判定
    
    i = 1
    result = []
    append!(result, [x])
    print(i, ":", x, " c:", c, "\n")
    
    while i==1 || norm( result[i-1] - result[i] ) > m
        i += 1
        c = ε*c
        SquarePenaltyProblem(x) = f(x) + c * max( 0, h(x) )^2
        x_next = GradientDescent(SquarePenaltyProblem, x, 0.05)
        append!(result, [x_next])
        print(i, ":", x_next, " c:", c, "\n")
        x = x_next
    end 
    
    return result
end

各ループで, $\mathrm{argmin} \left\{ f(\boldsymbol{x}) + c_k \max\left(0, \vec{h}(\boldsymbol{x})\right)^2 \right\}$ にあたる SquarePenaltyProblem() を定義し直してから GradientDescent() に与えています.

次に, 対数バリア法を同様に実装します.

function LogBarrier(f,h)
    x = (rand(2).+1)*20
    c = 10    #initialize
    ε = 0.5  # cの減衰率
    m = 0.01  # 収束判定
    
    i = 1
    result = []
    append!(result, [x])
    print(i, ":", x, " c:", c, "\n")
    
    while i==1 || norm( result[i-1] - result[i] ) > m
        i += 1
        c = ε*c
        logBarrierProblem(x) = f(x) - c * log( -h(x) )
        x_next = GradientDescent(logBarrierProblem, x)
        append!(result, [x_next])
        print(i, ":", x_next, " c:", c, "\n")
        x = x_next
    end 
    
    return result
end

それぞれ実行します.

SquarePenalty(f,h)

1:[33.5958, 39.9659] c:2
2:[0.0634654, 0.728719] c:4
3:[0.276879, 0.65636] c:8
4:[0.276879, 0.65636] c:16

LogBarrier(f,h)

1:[27.8908, 33.7221] c:10
2:[0.583505, 1.54771] c:5.0
3:[0.507339, 1.22301] c:2.5
4:[0.440713, 1.06398] c:1.25
5:[0.370418, 0.913105] c:0.625
6:[0.314403, 0.785594] c:0.3125
7:[0.314403, 0.785594] c:0.15625

解析解の $(x,y) = (0.4,0.6)$ とはややズレていますが, 概ねその近くに収束した……と言って良いのかなと思います.

*1:ラグランジュ双対問題を利用する解き方など他にも色々あるのですが, 長くなるので今回は割愛します

*2:「二次元平面で厳密に直線上に点を乗せること」などをイメージすると……

*3:バックトラック直線探索を行ったところ, 対数バリア法でバリアを突き抜けた位置に点が移動するなどしたため…

制約なし最適化問題における勾配法と, Julia によるバックトラック直線探索の実装

大学で受けた講義の復習として, 表題の内容について自分なりの理解でまとめます.

制約なし最適化問題

とは, 一般の$d$変数関数について, 以下のように定式化されるものでした.

$\mathcal{X} \subset \mathbb{R}^d$ 上の目的関数 $f:\mathcal{X}\mapsto\mathbb{R}$ の最小値を求めよ. $$ \min_{\vec{x}\in\mathcal{X}} f(\vec{x}) $$ ただし, $f$ は微分可能とする.

最大化問題は $f$ の符号を逆にすることで最小化問題になるので, 同じことです.

$f$ の定義域における制約条件（$\vec{x}$ に関する等式・不等式）が特にないので, 制約なし最適化問題です.

ここで, $f$の勾配を $\nabla f(\vec{x}) = \left(\dfrac{\partial f}{\partial x_1}, \dfrac{\partial f}{\partial x_2}, \ldots, \dfrac{\partial f}{\partial x_d} \right)^\mathrm{T}$ とすると, 以下の最適性条件

$\vec{x}^*$ が最適解 ならば $\nabla f(\vec{x}^*) = \vec{0}$

が成り立ちます. 関数がなめらかな場合, 最小値をとるときは必ず微分がゼロだという話です.

もちろん微分がゼロでも最小値をとるとは限らないのですが, $f$ が凸関数である場合, 「$\vec{x}^*$ が最適解」と「 $\nabla f(\vec{x}^*) = \vec{0}$」は同値になります.（凸最適化問題）

凸関数

「$f$は凸関数である」 とは,

$f$の定義域上の任意の$\vec{x}, \vec{x}'$に対して $$f((1-\theta)\vec{x}+\theta\vec{x}') \leq f((1-\theta)\vec{x})+f(\theta\vec{x}')$$

となることです. 「関数上のどの二点を結ぶ線分より関数の方が常に小さい」とも言えます.

また, $f$が一階微分可能な場合は, 上の定義は

$$ f(\vec{x}') \geq f(\vec{x}) + \nabla f(\vec{x})^\mathrm{T}(\vec{x}'-\vec{x}) $$

とも同値となります. 「任意の点における接線は, 常に関数自体より小さい」ということですね.

さらに, $f$ が二階微分可能な場合,

ヘッセ行列 $\nabla^{2} f(\vec{x})$の固有値が全て非負（ヘッセ行列が半正定値となる）

となることとも同値です. 一変数関数の場合の「二階微分が非負」であることに対応します.

前述の通り, $f$が凸関数である場合, 「 $\nabla f(\vec{x}^*) = \vec{0}$ ならば $\vec{x}^*$ が最適解」が成り立ちます.

(制約なし)最適化アルゴリズムは一般に「勾配がゼロになる点に収束するような点列を構成する」手続きといえるため, 凸関数であれば大域最適解が求まり嬉しいのですが, 凸でない関数だと 局所最適解しか得られません. その場合, 複数の初期値からアルゴリズムを実行して一番よいものを選ぶなどします.

勾配法（最急降下法）

代表的な最適化アルゴリズムが 勾配法（最急降下法） です. 勾配法は一般に以下の式で表されます.

適当な初期値から始め, 収束するまで以下を繰り返す : $$ \vec{x}_{k+1} \leftarrow \vec{x}_k - \varepsilon_k\nabla f(\vec{x}_k)$$

ここで $\varepsilon_k > 0$ はステップ幅と呼ばれる係数です.

要するに, $f$の勾配 $\nabla f(\vec{x}) = \left(\dfrac{\partial f}{\partial x_1}, \dfrac{\partial f}{\partial x_2}, \ldots, \dfrac{\partial f}{\partial x_d} \right)^\mathrm{T}$ は, ベクトルとしては「その点の近傍において, 最も関数値が増加する方向」を意味すると言えるので, 「各ターン, その位置から勾配の逆(減少)方向にいくらか進める」ことを繰り返すという戦略ですね.

ステップ幅 $\varepsilon_k > 0$ は大きすぎると収束しませんが, 小さすぎると収束が遅いです. これをどのように決めるかによって, 勾配法にはいくつか種類があります.

そのうちのひとつが以下で実装を示すバックトラック直線探索です.

アルミホ規準とバックトラック直線探索

バックトラック直線探索の定義をまず以下に示します.

勾配法 $$ \vec{x}_{k+1} \leftarrow \vec{x}_k - \varepsilon_k\nabla f(\vec{x}_k)$$ の各 $k$ において $\varepsilon_k $ を計算し直す.

$\varepsilon_k = 1$ と初期化したのち, アルミホ規準 : $$ f( \vec{x}_k - \varepsilon_k \nabla f(\vec{x}_k) ) - f(\vec{x}_k) \leq - \alpha \varepsilon_k || \nabla f(\vec{x}_k) ||^2 $$ が成り立つまで, $\varepsilon_k$を, $$\varepsilon_k \leftarrow \beta\varepsilon_k$$ を繰り返すことで減衰させる.

ここで, $0<\alpha, \beta<1$ は事前に定める定数である.

バックトラック直線探索とは, 勾配法の各ループでアルミホ規準というルールに従うように$\varepsilon_k$を選びなおすことで, 関数$f$の減少量に関してある保証を行うというアイデアに基づく勾配法です.

以下, アルミホ規準について見ていきます.

$$ f( \vec{x}_k - \varepsilon_k \nabla f(\vec{x}_k) ) - f(\vec{x}_k) \leq - \alpha \varepsilon_k || \nabla f(\vec{x}_k) ||^2 $$

左辺は, ある$ \varepsilon_k$が定まったとして, そのとき$ \vec{x}_{k+1} \leftarrow \vec{x}_k - \varepsilon_k\nabla f(\vec{x}_k)$と更新した場合の$f$の減少量であることがわかると思います.

問題は右辺なのですが, 結論から言うと, これは「$f$の減少量の線形予測値(の$\alpha$倍)」です.

前述の通り, 勾配法の$k$ステップにおける$f$の減少量は$\varepsilon_k$が定まれば一意に定まるので, $f$の減少量は, $\varepsilon_k$の関数

$$g(\varepsilon_k) = f( \vec{x}_k - \varepsilon_k \nabla f(\vec{x}_k) ) - f(\vec{x}_k)$$

として考えることができます. その上で, $\varepsilon_k=0$における微係数$g^{\prime}(0)$を, \begin{align} \left. \frac{\mathrm{d} g(\varepsilon_k) }{\mathrm{d} \varepsilon_k} \right|_{\varepsilon_k=0} &= \left. \left\{ - \nabla f(\vec{x})^{\mathrm{T}} \nabla f( \vec{x}_k - \varepsilon_k \nabla f(\vec{x}_k) ) \right\} \right|_{\varepsilon_k=0} \\ &= - \nabla f(\vec{x})^{\mathrm{T}} \nabla f(\vec{x}) \\ &= - || \nabla f(\vec{x}_k) ||^2 \end{align}

と計算すると, $f$の減少量$g(\varepsilon_k)$の線形予測値として, $$ \varepsilon_k g^{\prime}(0) = - \varepsilon_k || \nabla f(\vec{x}_k) ||^2 $$ を得ます.

以上のことから, アルミホ規準は,

少なくとも各ステップで, $f$の減少量の線形予測値の$\alpha < 1$倍は減少するようにする

ようなルールであることがわかります.

バックトラック直線探索の julia 実装

前置きが長くなりました. 実装しましょう. 使用するのは Julia 1.0.2 です.

今回も可視化に Plots + GR を用いることにします.

using LinearAlgebra
using Plots

gr()
ENV["PLOTS_TEST"] = "true"

また, 今回は簡単のため, 最適化を行う目的関数として,

$$ f(\vec{x}) = 10 x_1² + x_2² $$

を用いることにして, それを定義しておきます. 明らかに最適解は$(x_1, x_2)=(0,0)$でその値は$f(\vec{x}^*)=0$ですが, アルゴリズムの機能の仕方を可視化しながら観察するには単純であるほうがよいでしょう.

ついでに勾配を返す関数も定義します（都合から二変数に限ってしまいましたが）

function f(x)
    return 10x[1]^2 + x[2]^2
end

function ∇(f,x)
    h = 0.0001
    return [( f(x+[h,0]) - f(x-[h,0]) ) / 2h, 
            ( f(x+[0,h]) - f(x-[0,h]) ) / 2h]
end

勾配関数∇はあるものとして, 目的関数$f$と$\alpha, \beta$を入力として受け取って, バックトラック直線探索を行って得られた$\vec{x}$および$f(\vec{x})$の列を出力します. ここではデバッグのため各ループでも値をプリントさせるようにしました.

function BTLSGradientDescent(f, α=0.5, β=0.8)
    x = (rand(2).-0.5).*10
    i = 0
    ε = 1
    m = 0.1
        
    x_seq = zeros(0)
    f_seq = zeros(0)
    append!( x_seq, x )
    append!( f_seq, f(x) )
    print(i,":",x," f:",f(x),"\n")
    
    while abs(norm( ∇(f,x) - ∇(f,x - ε.*∇(f,x)) )) > m
        if f(x - ε.*∇(f,x)) - f(x) <= -α*ε.*norm(∇(f,x))  # Armijo
            x = x - ε.*∇(f,x)
            ε = 1
            i += 1
            print(i,":",x," f:",f(x),"\n")
            append!( x_seq, x )
            append!( f_seq, f(x) )
        else
            ε = β*ε
        end
    end
    return reshape(x_seq, 2,:), f_seq
end

実行結果は以下です. $f$が最小値$0$に収束するのがわかります.

x_seq, f_seq = BTLSGradientDescent(f)

0:[2.67815, 2.54762] f:78.21508380277415
1:[-1.92287, 2.10994] f:41.426324107210576
2:[1.3806, 1.74746] f:22.114138557399237
3:[-0.991252, 1.44725] f:11.920326667200023
4:[0.711706, 1.19861] f:6.501923402334815
5:[-0.510995, 0.992693] f:3.5966018700862796
6:[0.366888, 0.822149] f:2.0219977430959752
7:[-0.263421, 0.680905] f:1.1575369871905883
8:[0.189133, 0.563926] f:0.6757248514793868
9:[-0.135795, 0.467045] f:0.4025329889285466
10:[0.0974989, 0.386807] f:0.24467998560906534
11:[-0.0700029, 0.320354] f:0.1516308200203651
12:[0.0262084, 0.276325] f:0.08322424811647708
13:[-0.00260804, 0.245943] f:0.06055581977627555

([2.67815 -1.92287 … 0.0262084 -0.00260804; 2.54762 2.10994 … 0.276325 0.245943], [78.2151, 41.4263, 22.1141, 11.9203, 6.50192, 3.5966, 2.022, 1.15754, 0.675725, 0.402533, 0.24468, 0.151631, 0.0832242, 0.0605558])

この結果を可視化すると, 以下のようになります.

g(x, y) = begin
    10x^2 + y^2
end
a = b = -5:0.1:5
X = repeat(reshape(a, 1, :), length(b), 1)
Y = repeat(a, 1, length(b))
Z = map(g, X, Y)
p = contour(a, b, Z)
px = plot(p)

plot!(px,x_seq[1,:],x_seq[2,:],m=3,label="x")
annotate!(px,x_seq[1,:],x_seq[2,:].-0.1, [text(i,:top,8) for i in 1:length(x_seq[1,:])])

pf = plot(f_seq, m=2, label="f(x)", xticks=1:length(x_seq[1,:]), xlabel="iteration")

plot(pf,px,layout=(1,2),wsize=(1200,400))

Python3 & OpenCV で画像処理を学ぶ[7] 〜 エッジを保存する平滑化フィルタ

1. はじめに

前回

optie.hatenablog.com

は線形フィルタによるたたみこみで平滑化を行いました。

しかし、平均を用いた平滑化は全体が一様にぼけるため, エッジが失われてしまいます。

そこで今回は, エッジを保存したまま平滑化を行う方法を見ていきます。

2. エッジ保存平滑化

2.1. 下準備

いつものように, 必要なライブラリなどをインポートしていきます。

import cv2
import numpy as np
from numpy.lib.stride_tricks import as_strided
from matplotlib import pyplot as plt
import seaborn as sns

%config InlineBackend.figure_format = 'retina'

def imshow2(img1,img2, title1=None, title2=None):
    fig = plt.figure(figsize=(20,15))
    ax1 = fig.add_subplot(121)
    ax2 = fig.add_subplot(122)
    ax1.imshow(img1)
    ax2.imshow(img2)
    if title1:
        ax1.set_title(title1)
    if title2:
        ax2.set_title(title2)
    ax1.set_xticks([]), ax1.set_yticks([])
    ax2.set_xticks([]), ax2.set_yticks([])
    plt.show()

photo = cv2.cvtColor(cv2.imread('img_src/IMGP2769.jpg',1),cv2.COLOR_BGR2RGB)
wiz = cv2.cvtColor(cv2.imread('img_src/Wizdomiot.png',1),cv2.COLOR_BGR2RGB)

2.2. メディアンフィルタ

メディアンフィルタは, 目的のピクセルの周囲の画素値の中央値を出力とします。

中央値というのは, 例えば,

nums = np.random.randint(1,100,19)
print(nums)

[59  2 94 97 59  8 17 59 61 86 84 20 70  2 90 58  3  5 51]

このような数字の列を考える場合,

print(np.sort(nums))

[ 2  2  3  5  8 17 20 51 58 59 59 59 61 70 84 86 90 94 97]

このように昇順にソートしたときに,

np.median(nums)

59.0

ちょうど中央に来る値のことです。中央が存在しない場合、中央付近の2つの平均を出力とします。

メディアンフィルタは非線形フィルタです。中央値の計算はソートが入ってくるため, 平均値の計算のようにカーネルとの積和の形に書き直すことができず, 前回扱ったような線形フィルタでは実現できないことがわかると思います。

opencvでは cv2.medianBlur(img,size) で利用できます。使ってみましょう。

med = cv2.medianBlur(wiz,19)
imshow2(wiz,med,"ref", "filtered")

やや強くかけてみました。魔法陣が溶けた、あるいはにじんだような効果が得られています。

ところで、メディアンフィルタの本来の用途はノイズの除去であるようです。 そこで、やや恣意的ですが, 以下にノイズをかけた画像を用意しました。

noise = np.random.binomial(1,0.95,photo.shape[:2])[:,:,np.newaxis].repeat(3,axis=2)
noised_photo = (photo * noise).astype('uint8')
plt.figure(figsize=(10,7.5))
plt.imshow(noised_photo)
plt.show()

これにメディアンフィルタをかけてみます。

med = cv2.medianBlur(noised_photo,3)
imshow2(noised_photo,med, "ref", "filtered")

かなり綺麗に除去できています。中央値が外れ値に強いことを利用した方法ですね。

2.3. バイラテラルフィルタ

バイラテラルフィルタは, 「画素値の差」と「画素間の距離」に応じた重み付けを行って平滑化をするフィルタで、以下の式で表されます。

$P_{in}(x,y)$を入力, $P_{Out}(x,y)$を出力として,

ただし,
$w$ :カーネルサイズ, : 画素間距離の分散, : 画素値の分散

一見ちょっと地獄みたいな式ですが, 前回扱った二次元正規分布の発展形です。

平均:0, 分散:の二次元正規分布:

これを思い出しながらバイラテラルフィルタの式を分解して考えると,

まず,

は, 画素値間の距離に応じた正規分布の重みと考えることができます。

すなわち, 出力の画素 $P_{out}(x,y)$ と同じ位置 ($i=j=0$) なら $e^0=1$ で重みが最大になり, $(x,y)$から離れるほど小さい値になります。

次に,

は, 画素値の差の大きさに応じた重みです。

$\big(P_{in}(x,y) - P_{in}(x+i, y+j)\big)^2 = 0$, すなわち注目している $P_{in}(x,y)$ の画素値と $P_{in}(x+i, y+j)$ が同じであれば, $e^0=1$ で重みが最大になり, 画素値の差が開くほど小さい重みになります。

ここから, は遠方の画素値の影響度を制御していて, は差の大きい値の影響度を制御していると見ることができます。

opencvでは cv2.bilateralFilter(img, size, sigma1, sigma2) で利用できます。

これを画像に繰り返し適用してみます。

photo2 = cv2.cvtColor(cv2.imread('img_src/IMGP2794.jpg',1),cv2.COLOR_BGR2RGB)

b1 = cv2.bilateralFilter(photo2,5,40,40)
imshow2(photo2,b1, "ref", "bilateral:1")

for i in range(11):
    b1 = cv2.bilateralFilter(b1,5,40,40)
    b2 = cv2.bilateralFilter(b1,5,40,40)
    imshow2(b1,b2,"bilateral:"+str((i+1)*2),"bilateral:"+str((i+1)*2+1))
    b1 = np.copy(b2)

(中略)

あまり良い例ではなかった気もしますが, エッジを保ちつつぼかしがかかっていることがわかると思います。

2.4. 最大値・最小値フィルタ

先ほど中央値を扱ったので, 他の統計量について見てみます。試しに、最大値と最小値でフィルタリングをしてみたいと思います。面白い効果が得られると嬉しいです。

知る限り、最大値と最小値を返すフィルタはopencvにはない(あるかも)ので, 前回書いた畳み込み演算の関数を改造して, 非線形フィルタ用の関数を作ってみます。

def nonlinear_convolve2d(img, f, size, padding='0'):
    out_shape = img.shape
    if len(img.shape) != 2:
        print('img should be 2d-array')
        return
    if size%2 == 0:
        print('Kernel size shold be odd')
        return
    
    edge = int(size/2)
    
    if padding=='edge':
        img = np.pad(img, [edge,edge], mode='edge')
    elif padding=='reflect':
        img = np.pad(img, [edge,edge], mode='reflect')
    else:
        img = np.pad(img, [edge,edge], mode='constant', constant_values=0)
    
    sub_shape = tuple(np.subtract(img.shape, (size, size)) + 1)

    conv_shape = sub_shape + (size, size)

    strides = img.strides + img.strides

    submatrices = as_strided(img, conv_shape, strides)

    convolved_mat = np.apply_over_axes(f, submatrices, [2,3]).reshape(out_shape)
    
    return convolved_mat

まず, 最大値を使ってみます。

max_filtered = np.zeros(photo.shape)
for (i, ch) in enumerate(['R','G','B']):
    max_filtered[:,:,i] = nonlinear_convolve2d(photo[:,:,i], np.max, 7, padding='edge')
max_filtered = max_filtered.astype('uint8')
imshow2(photo, max_filtered)

陰影が落ちたかのような独特な効果が得られました。

次に, 最小値でフィルタリングを行ってみます。

min_filtered = np.zeros(photo.shape)
for (i, ch) in enumerate(['R','G','B']):
    min_filtered[:,:,i] = nonlinear_convolve2d(photo[:,:,i], np.min, 7, padding='edge')
min_filtered = min_filtered.astype('uint8')
imshow2(photo, min_filtered, "ref", "filtered")

どこかドット絵っぽい?雰囲気になりました。

最大値・最小値フィルタは領域ごとに同じような値が返るためか, 角っぽい感じになっています。

そこで, これらの上に更にメディアンフィルタをかけてみます。

med = cv2.medianBlur(max_filtered,11)
imshow2(max_filtered,med,"ref", "filtered")

med = cv2.medianBlur(min_filtered,11)
imshow2(min_filtered,med,"ref", "filtered")

最小値・最大値フィルタの角が丸められた関係で, 絵画っぽくなった気がします。

3. まとめ

今回は、メディアン・バイラテラルなどの非線形フィルタを用いてエッジを保存する平滑化の概念とやり方を学びました。

次回はエッジ抽出をやります。

4. 参考文献

• 「ディジタル画像処理」の6章

Julia言語と Plots + GR で複素関数のgifアニメーションを作る

1. この記事について

やりたいこと

　最近, 趣味で複素解析の初歩などを勉強しているのですが, ある複素数 $z,w$を

$ \begin{cases} z=x+yi \\ w=u+vi \end{cases} $

とおくと, 複素関数 $w=f(z)$ は, 二変数に二変数が対応する関数

$f:(x,y)\rightarrow(u,v)$

になります。素直にその様子を描こうとすると4次元のグラフが必要ですが, それは不可能です。そのため, 複素関数はそのふるまいを直観的に理解することがやや難しいです。

複素関数の様子を知ろうとすると, 基本的には, 「x-y平面上の点や直線や円などの基本的な図形が, 関数によってu-v平面にどのように写されるか？」を考えることになるのですが, それにしても情報は落ちているので, 様子を把握するには慣れが必要そうな感じがします。

　そこで, 本記事では, いくつかの複素関数に対し, 「x-y平面上で図形をアニメーションさせて, それがu-v平面上でどのように動くか」を見ることで, 複素関数に対する理解を深めていきたいと思います。

やること

　複素関数のプロットとアニメーションということで, いつも通りPythonでも良いのですが, せっかくなので Julia という言語を初めて使ってみることにします。

(出展: https://github.com/JuliaLang/julia)

https://julialang.org/

　Julia とは, 数値計算・科学技術計算用に作られた言語で, 計算が非常に高速であることで知られています。

　また, 言語仕様がシンプルで, Python以上にすっきりしたコードを書くことができたり, 非常に強力な標準ライブラリやマクロ機能を備えていたり, Pythonなどを簡単に呼び出せるために他の資産の利用が容易などといった特徴があるようです。もちろん, Jupyter notebookで利用することもできます。

　言語としてはまだ若く, 利用者もPythonに比べてまだまだ多くはないのですが, 今後非常に将来性がありそうな感じがしています。

　ということで, 今回はタスク自体は簡単そうということもあり, この機に習得してみたいと思います。

2. 下準備

　Julia 本体(および Python, jupyter notebook )はインストール済みであるものとします。 Juliaのインストールについては以下などを参考。

Julia v0.6.1のインストールとJupyter Notebookで使うまで - Qiita

パッケージのインストール

Pythonなどと同様, ターミナル上などでjuliaを起動するとjuliaのREPLが開くので, そこでPkg.add() で利用したいパッケージ名を入力します。

その後, Pkg.update() を行い, アップデートなどを確認するのが一般的なパッケージ導入の流れです。

今回は以下のパッケージを利用しました。

Pkg.add("Ijulia")
Pkg.add("Plots")
Pkg.add("GR")
Pkg.add("LaTeXStrings")
Pkg.add("ProgressMeter")
Pkg.update()

それぞれ以下に解説します。

IJulia

Jupyterでjuliaを利用するためのカーネル。Pkg.add("Ijulia") とするだけで使えるようになる。

Plots

Juliaで標準的な, 描画用ライブラリのフロントエンド(インターフェース)。 pyplotやGRなどといったバックエンドと組み合わせて使う。

GR

JuliaでしばしばPlotsのバックエンドとして用いられる描画用パッケージ。C/C++で書かれているらしく, かなり速い。

LaTeXStrings

L"z=x^2" など書くことで, Plotsなどに渡した文字列が LaTeX文字列と認識され, $z=x^2$ というように表示されるようになる。(しかしあまり綺麗に出なかったので今回使わなかった)

ProgressMeter

ループなどを回すときに, 進捗メーターを表示させるためのパッケージ。

3. プロット & アニメーション

importとヘルパー関数など

Juliaでのモジュールのインポートは以下のようにします。

using Plots
import ProgressMeter
using LaTeXStrings

import と using がありますが, 以下のような違いがあるようです。

　例えば, import Plots とすると, Plots モジュール内の plot() 関数を, Plots.plot() と書くことで呼び出せるようになります。また, import Plots.plot などと書けば,Plots. を省略して plot() と書くことができます。これはPythonのimportと同じですね。

　using Plots とする場合, モジュール自体に加えて Plots モジュールの名前空間ごと Main に持ってくるため, Plots.plot()関数であればPlots. を省略して plot() と書くことができます。ただし, 関数名などが衝突する恐れがあると警告が出るようです。

以下は指定ディレクトリにあるgifファイルを読み込んで jupyter 上で表示するための関数です。 先にgifを生成してから, この関数を使用して表示します。

# open ... do ... endはdoの中でエラーが起きても必ずファイルを閉じる
displayfile(mime, file) = open(file) do stream
    base64 = base64encode(stream)
    display("text/html", """<img src="data:$mime;base64,$base64">""")
end

Plotsをimportして, 以下のように書けばGRバックエンドが立ち上がり, 後は plot() などの関数を実行することでプロットすることができます。

gr()

しかし, 最新版の GR を使うと, なぜか出力の画像サイズが指定の6倍になってしまうという仕様があります。そこでENV["PLOTS_TEST"] = "true" と書くことでこれを無効にします。

ENV["PLOTS_TEST"] = "true"

例1. $z=w^2$

まずは練習も兼ねて, $z=w^2$ をプロットします。

gr(
    legend=false,
    titlefont=Plots.font("sans-serif", 12),
    legendfont=Plots.font("sans-serif", 8),
    guidefont=Plots.font("sans-serif", 10),
    tickfont=Plots.font("sans-serif", 8),
    markersize=4, markerstrokewidth = 1, 
    markercolor= "#FF445B",markerstrokecolor="#4A4A4A",
    linewidth=2
)

n = 100  # フレーム数
prog = ProgressMeter.Progress(n,1)


anim = @animate for i in linspace(-10,10,n)
    k = i

    x1 = linspace(-50,50,201)
    y1 = k
    z1 = x1 + y1*im

    x2 = k
    y2 = linspace(-50,50,201)
    z2 = x2 + y2*im
    
    z3 =  k + k*im

    w1 = z1.^2
    w2 = z2.^2
    w3 = z3.^2

    p1 = plot(real(z1), imag(z1), linecolor="#F5A623", lims=(-20,20), title="x-y")
    plot!(p1, real(z2), imag(z2), linecolor="#4A90E2")
    vline!(p1,[0],line=(:black, 1)) # y軸
    hline!(p1,[0],line=(:black, 1)) # x軸
    scatter!(p1, (real(z3),imag(z3)))


    p2 = plot(real(w1),imag(w1), linecolor="#F5A623",  lims=(-200,200), title="u-v")
    plot!(p2, real(w2),imag(w2), linecolor="#4A90E2")
    vline!(p2,[0],line=(:black, 1))
    hline!(p2,[0],line=(:black, 1))
    scatter!(p2, (real(w3),imag(w3)))
    
    plot(p1,p2,size=(800,350), plot_title=L"w=z^2")
    
    ProgressMeter.next!(prog)
end


dir = "/"
fps = 30
filename = "01_fps$fps.gif"

gif(anim, filename, fps = fps)

displayfile(dir,filename)

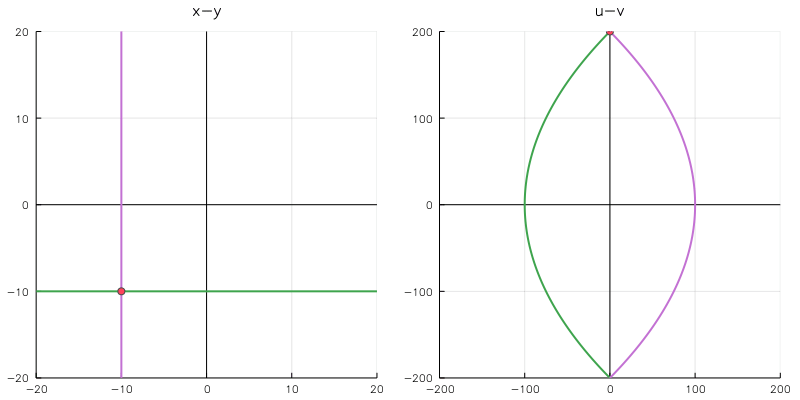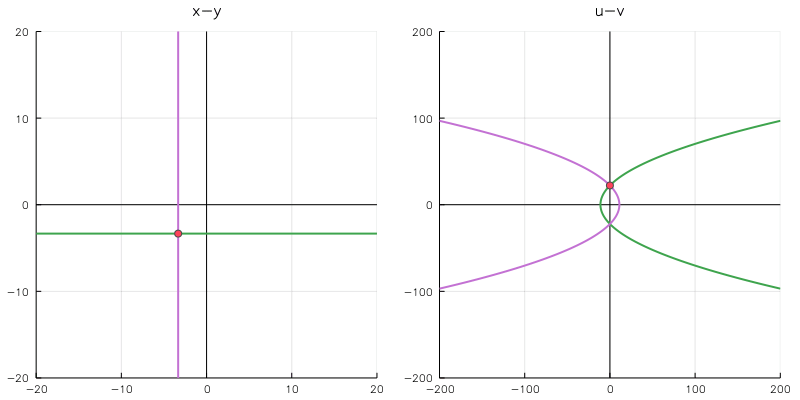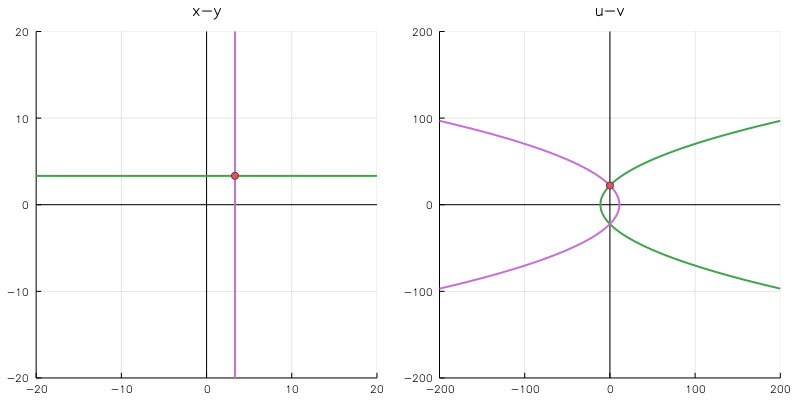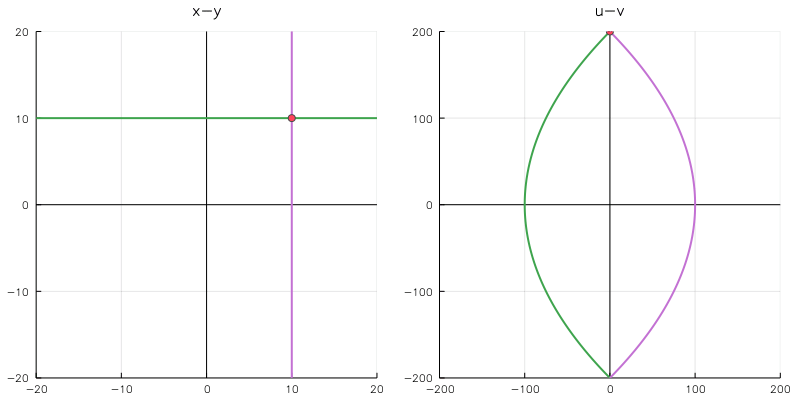
これは有名な例ですが, $z=w^2$ は,

$ \begin{cases} z=x+yi \\ w=u+vi \end{cases} $

とおくと, $w = z^2 = x^2-y^2+2xyi$ より,

$ \begin{cases} u=x^2-y^2 \\ v=2xy \end{cases} $

となります。$x,y$ をそれぞれ固定して考えると, u-v平面では横倒しの二次関数の形となるため, プロットのように直線が二次関数に写されます。

また, x-y 平面で直交する二直線は, u-v 平面の二次関数に写されても互いに直交することが確認できます。

関数化

これらの処理を関数化してみます。任意の複素関数と, 定数kに応じて変化する図形群を与えられるようにします。

# 複素関数 f, 定数kを受け取り複素数列(点群)を返す shape の配列 shapes
function makeanim(f, shapes; n=100, kmin=-10, kmax=10, zsize=10, wsize=10, unitcircle=true)
    prog = ProgressMeter.Progress(n,1)
    
    anim = @animate for i in linspace(kmin,kmax,n)
        
        p1 = plot(lims=(-zsize, zsize), title="x-y")
        p2 = plot(lims=(-wsize, wsize), title="u-v")
        vline!(p1,[0],line=(:black, 1))
        hline!(p1,[0],line=(:black, 1))
        vline!(p2,[0],line=(:black, 1))
        hline!(p2,[0],line=(:black, 1))    
        
        if unitcircle
            θ = linspace(0,2π,60)
            plot!(p1, sin.(θ), cos.(θ), line=(:black, 1))
            plot!(p2, sin.(θ), cos.(θ), line=(:black, 1))
        end
            
        
        k = i
        
        for shape in shapes
            z = shape(k)
            w = f(z)
            
            if length(z)>1  # 点ならscatterを使う
                plot!(p1, real(z), imag(z))
            else
                scatter!(p1, (real(z),imag(z)))
            end
            
            if length(w)>1
                plot!(p2, real(w),imag(w))
            else
                scatter!(p2, (real(w),imag(w)))
            end
            
        end
        
        plot(p1,p2,size=(800,400))
        ProgressMeter.next!(prog)
        
    end
    
    return anim
    
end

図形は以下のようにします。

function yline(k)
    x = linspace(-50,50,1001)
    y = k
    z = x + y*im
end

function xline(k)
    x = k
    y = linspace(-50,50,1001)
    z = x + y*im
end

function xylinecrosspoint(k)
    x = k
    y = k
    z = x + y*im
end

function circle(k)
    r = k
    θ = linspace(-π,π,10000)
    z = r*(cos.(θ) + im*sin.(θ))
end

function circleline(k)
    r = linspace(0,100,10001)
    θ = 2k
    z = r*(cos.(θ) + im*sin.(θ))
end

function circlepoint(k)
    r = k
    z = r*(cos.(2k) + im*sin.(2k))
end

これらを以下のように使います。

function f1(z)
    z.^2
end

shapes=[yline, xline, xylinecrosspoint]
anim = makeanim(f1, shapes, zsize=20, wsize=200, unitcircle=false)

dir = "/"
fps = 30
filename = "01_fps$fps.gif"

gif(anim, filename, fps = fps)

displayfile(dir,filename)

出力は省きますが, 色を除いて上記と同じ結果となります。

例2. $w=\frac{1}{z}$

function f2(z)
    1./z
end

shapes1=[yline, xline, xylinecrosspoint]
shapes2=[circle, circleline, circlepoint]

dir = "/"
fps = 30
filename1 = "02_1_fps$fps.gif"
filename2 = "02_2_fps$fps.gif"

anim1 = makeanim(f2, shapes1, n=150, kmin=-2, kmax=2, zsize=2, wsize=2)
gif(anim1, filename1, fps = fps)
displayfile(dir,filename1)

anim2 = makeanim(f2, shapes2, n=250, kmin=2π, kmax=0, zsize=2π, wsize=2π)
gif(anim2, filename2, fps = fps)
displayfile(dir,filename2)

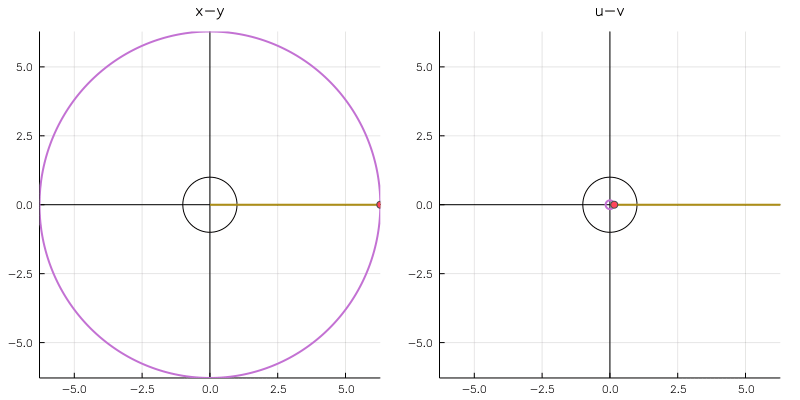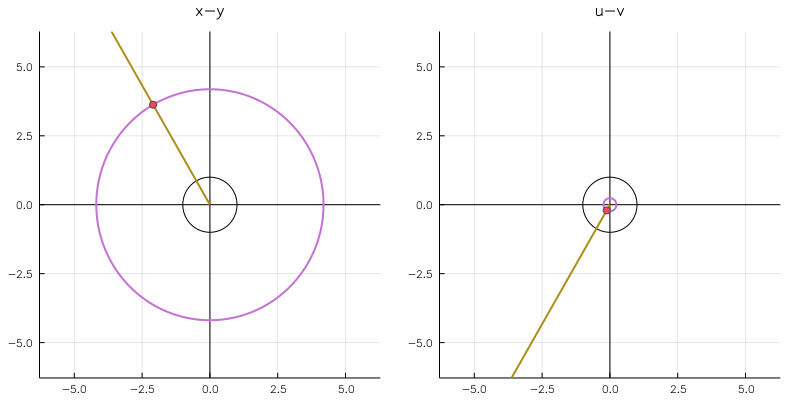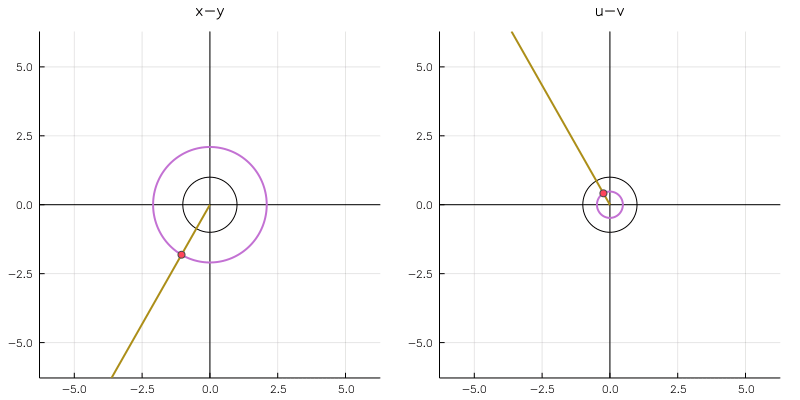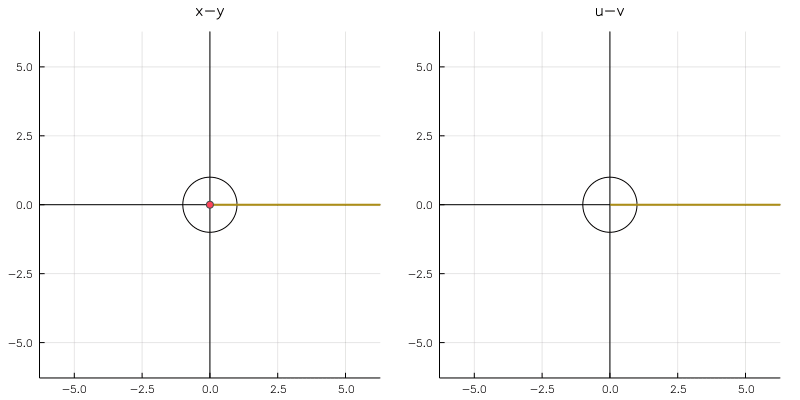
実軸対称 + 単位円に関して対称なやつです。直線の方は原点付近でリーマン球面をぐるりと回り込んでいますね。

例3. $w= \sin z$

function f3(z)
    sin.(z)
end

dir = "/"
fps = 30
filename1 = "03_1_fps$fps.gif"
filename2 = "03_2_fps$fps.gif"

anim1 = makeanim(f3, shapes1, n=150, kmin=-2, kmax=2, zsize=2, wsize=2)
gif(anim1, filename1, fps = fps)
displayfile(dir,filename1)

三角関数です。この辺は円を入れると異常な動きになります(よくわからない)。

anim2 = makeanim(f3, shapes2, n=500, kmin=π, kmax=0, zsize=2π, wsize=2π)
gif(anim2, filename2, fps = fps)
displayfile(dir,filename2)

例4. $w=\tan z$

function f4(z)
    tan.(z)
end

dir = "/"
fps = 30
filename1 = "04_1_fps$fps.gif"
filename2 = "04_2_fps$fps.gif"

anim1 = makeanim(f4, shapes1, n=150, kmin=-2, kmax=2, zsize=2, wsize=2)
gif(anim1, filename1, fps = fps)
displayfile(dir,filename1)

anim2 = makeanim(f4, shapes2, n=500, kmin=π, kmax=0, zsize=2π, wsize=2π)
gif(anim2, filename2, fps = fps)
displayfile(dir,filename2)

例5. $w=e^z$

function f5(z)
    e.^z
end

dir = "/"
fps = 30
filename1 = "05_1_fps$fps.gif"
filename2 = "05_2_fps$fps.gif"

anim1 = makeanim(f5, shapes1, n=150, kmin=-2, kmax=2, zsize=2, wsize=2)
gif(anim1, filename1, fps = fps)
displayfile(dir,filename1)

直線が円に写ります。x-y平面の紫の線は, $2\pi$ 上下にずらしてもu-v平面で同じ線に写ります。

anim2 = makeanim(f5, shapes2, n=500, kmin=π, kmax=0, zsize=2π, wsize=4π)
gif(anim2, filename2, fps = fps)
displayfile(dir,filename2)

例6. $w = \log z$

function f6(z)
    log.(z)
end

dir = "/"
fps = 30
filename1 = "06_1_fps$fps.gif"
filename2 = "06_2_fps$fps.gif"

anim1 = makeanim(f6, shapes1, n=150, kmin=-2, kmax=2, zsize=2, wsize=2)
gif(anim1, filename1, fps = fps)
displayfile(dir,filename1)

$w=e^z$の逆で, 円が直線に写ります。u-v平面では黄色い線は $2\pi$ おきに無限に繰り返されます。

例7. $w= \mathrm{sin{h}} z$

function f7(z)
    sinh.(z)
end

dir = "/"
fps = 30
filename1 = "07_1_fps$fps.gif"
filename2 = "07_2_fps$fps.gif"

anim1 = makeanim(f7, shapes1, n=150, kmin=-2, kmax=2, zsize=2, wsize=2)
gif(anim1, filename1, fps = fps)
displayfile(dir,filename1)

anim2 = makeanim(f7, shapes2, n=200, kmin=π, kmax=0, zsize=π, wsize=π)
gif(anim2, filename2, fps = fps)
displayfile(dir,filename2)

$ \mathrm{sin{h}} z$ の定義より, $w=\sin z$の$z$に$i$をかけて回転させたものになります。

例8. $w=z^\frac{1}{3}$

function f8(z)
    z.^(1/3)
end

dir = "/"
fps = 30
filename1 = "08_1_fps$fps.gif"
filename2 = "08_2_fps$fps.gif"

anim2 = makeanim(f8, shapes2, n=200, kmin=π, kmax=0, zsize=π, wsize=π)
gif(anim2, filename2, fps = fps)
displayfile(dir,filename2)

x-y平面の円全体がu-v平面の$\frac{1}{3}$の扇状の領域に対応します。

4. まとめ

　複素関数のふるまいについて理解が深まりました。また, Juliaの書き方とプロットのやり方がわかりました。

Python+matplotlibよりかなり高速で使いやすいので, 今後も使っていきたいです。

5. 参考文献

• GitHub - bicycle1885/Julia-Tutorial: 高速でJuliaを学ぶチュートリアル
• Home · The Julia Language
• Plots http://docs.juliaplots.org/latest/
• Plots/GR: グラフ package のおすすめ · julia について
• http://nbviewer.jupyter.org/gist/genkuroki/3d6dbf52a3e52eb7c664bc88632c81d3#Plots.gr()-%E3%81%AB%E3%82%88%E3%82%8BGIF%E3%82%A2%E3%83%8B%E3%83%A1%E4%BD%9C%E6%88%90

Python3 & OpenCV で画像処理を学ぶ[6] 〜 numpy で畳み込み演算と平滑化フィルタの実装

1. はじめに

　今回は、空間フィルタリングの基礎概念に触れて、いくつかの平滑化フィルタを実装します。

　理解を深めるため, まず畳み込み演算から自力でnumpyで実装し, 次にOpenCVでのやり方と比較するという過程を踏みます。

2. 基本概念

2.1. 空間フィルタリングとは

　これまで触れてきたヒストグラム, トーンカーブ, 描画モードなどは, あくまで「ピクセルごと」のお話でした。つまり, 画像データでは本来, 「どのピクセルがどこにあるか」「隣接するピクセルは何か」などの位置に関わる情報も重要であるはずなのですが, そういったことは一旦無視した話だったというわけです。

　そこで, 画像に対して「隣接するピクセルを考慮した変換」をしたくなります。そのような変換を「空間フィルタリング」と呼びます。 具体例としては, 以下のようなものがあります。

• ブラー（画像処理では「平滑化」の一種. 今回扱います）
• メディアン
• 輪郭検出
• シャープネス

2.2. 畳み込み演算とは

　そこで行われるのが, 畳み込み Convolution と呼ばれる演算です。これはどのような演算でしょうか。

　まずは一次元配列で考えてみます。まず, 入力の配列の他に, カーネルと呼ばれるフィルタ(配列)を以下のような位置に用意します。

次に, カーネルの要素と, 同じ位置にある入力の要素とをそれぞれ掛けて, それらを足し合わせたものを, カーネルの中心の直下の出力の値とします。

( 3×1 + 1×2 + 2×1 = 7 )

そして, カーネルをひとつ隣に動かして, 再び先ほどの計算を行います。これを全マスで行うことで, 出力が得られます。

当然ながら, カーネルが偶数サイズだと真ん中が存在しないので, カーネルは奇数サイズである必要があります。

また, これでは入力の一番端にあたるマスの出力が計算できない気がしてきますが, その場合は以下のような方法で対処します。

• 必要なマスを 0 で埋める(ゼロパディング)
• 最端にある値を繰り返す
• 画面端を境に対称となるように, 反転しながら繰り返す

　以上をまとめると, 畳み込みとは以下のような演算ということになります。

1. なんらかの形で入力の端を延長する。
   
2. 入力 と カーネル の対応する値を掛けて総和をとることで, カーネル直下の出力の値を一つ得る。
   
3. カーネルを端から端まで動かしながら, 全てのマスでこの計算を行う。
   

　画像については, これをそのまま二次元配列に拡張すればよいです。以下のようなイメージですね。

　これからまた具体的に見ていきますが, この畳み込み演算で用いるカーネルの値によって, ブラーがかかったりエッジを抽出したりなど, 様々な効果が生まれるということです。

　また, 以上のような「カーネルの値と画素値 の積和」という計算によってのみ構成されるフィルタを線形フィルタと呼び, そうでない式を含むフィルタを非線形フィルタと呼ぶようです.

3. 平滑化の実装

import numpy as np
from numpy.lib.stride_tricks import as_strided
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import axes3d
import matplotlib.gridspec as gridspec
import seaborn as sns
import cv2

%config InlineBackend.figure_format = 'retina'

3.1. 平均化フィルタ

　平均化フィルタは, あるピクセルの周囲の画素値の平均値を出力とするフィルタです。

　例えば, 以下のようなカーネルを用います。

kernel = np.ones([3,3]) / (3*3)
print(kernel)

[[ 0.11111111  0.11111111  0.11111111]
 [ 0.11111111  0.11111111  0.11111111]
 [ 0.11111111  0.11111111  0.11111111]]

要するに, 和が 1 になるように, 各マスに均等な値を用います。 5×5なら以下の通りです。

N = 5 # should be odd
kernel = np.ones([N,N]) / (N*N)
print(kernel)

[[ 0.04  0.04  0.04  0.04  0.04]
 [ 0.04  0.04  0.04  0.04  0.04]
 [ 0.04  0.04  0.04  0.04  0.04]
 [ 0.04  0.04  0.04  0.04  0.04]
 [ 0.04  0.04  0.04  0.04  0.04]]

平均とは, 以下のようなものだったことを思い出すと,

$ \dfrac{a_1 + a_2 + … + a_N}{N} $

このようなカーネルによる畳み込み演算の出力は, 周囲の画素値の平均値となっていることがわかります。

3.1.1 python/numpy による実装

　さっそく, 畳み込み演算による平均化フィルタを実装してみたいと思います。まずは OpenCV に頼らず, numpy で畳み込み演算を実装してみることにします。

　そのために, 先ほど from numpy.lib.stride_tricks import as_strided として読み込んでいた numpy.lib.stride_tricks.as_strided() という関数を用いると便利です。

　これは, ある numpy.ndarray から, 要素を抜き出した view を作ることができる関数です。 view とはつまり, 新たな配列を実体として作るのではなく, 元の array が確保したメモリ上の値を参照する配列です。 view の要素の値を書き換えると, 元の array の値も変更されます。

　また, numpy.ndarray は, 本来 C の配列のようにメモリ上で連続して確保されています。そこで, この関数を用いることで, 一定 byte 間隔(stride)で値を抜き出してくる, といったことができます。

実装の基本方針としては以下の通りです。

例えば, (1280,720) のimg配列に対する (3,3) のカーネルの畳み込み演算では, as_strided を用いて (1280, 720, 3, 3) の配列を作ります。 (1280,720) の配列が, 畳み込みに備えた (3,3) 配列を要素として持つイメージです。

さて, そうして実装した畳み込み演算が以下になります。

まずはいつも通り, 画像表示用の関数。

def img_show2(img1,img2,titles=['ref_img','filtered']):
    fig = plt.figure(figsize=(20,7))
    ax1 = fig.add_subplot(121)
    ax2 = fig.add_subplot(122)
    
    ax1.set_title(titles[0]), ax2.set_title(titles[1])
    
    ax1.set_xticks([]), ax1.set_yticks([])
    ax2.set_xticks([]), ax2.set_yticks([])
    
    ax1.imshow(img1)
    ax2.imshow(img2)
    
    plt.show()

次に, imgとkernelを受け取って畳み込みをした配列を返す関数です。imgが3次元配列だとややこしくなるので, グレースケールもしくはRGB各チャンネルごとに利用することを想定しています。

def convolve2d_1ch(img, kernel, padding='0'):
    # エラー処理
    if len(img.shape) != 2:
        print('img should be 2d-array')
        return
    if kernel.shape[0]%2 == 0:
        print('Kernel size shold be odd')
        return
    
    edge = int(kernel.shape[0]/2)
    
    # 境界をどうするか
    if padding=='edge':
        img = np.pad(img, [edge,edge], mode='edge')
    elif padding=='reflect':
        img = np.pad(img, [edge,edge], mode='reflect')
    else:
        img = np.pad(img, [edge,edge], mode='constant', constant_values=0)
    
    sub_shape = tuple(np.subtract(img.shape, kernel.shape) + 1)

    # (rows, cols, N, N)
    conv_shape = sub_shape + kernel.shape

    # A.strides は (Aのrow方向の一要素ごとのbytes数, col方向のbytes数) のタプル
    # (shape[0]*bytes, bytes, shape[0]*bytes, bytes)
    strides = img.strides + img.strides

    submatrices = as_strided(img, conv_shape, strides)

    # (i,j)配列と(k,l,i,j)配列で, (i,j)要素同士の積和を要素とした(k,l)配列を返す
    convolved_mat = np.einsum('ij, klij->kl', kernel, submatrices)
    
    return convolved_mat

これらを29×29のカーネルを用いて実際に実行すると, 以下のようになります。

img = cv2.cvtColor(cv2.imread('img_src/wizdomiot.png',1), cv2.COLOR_BGR2RGB)

N = 29
kernel = np.ones([N,N]) / (N*N)

mean_convolved = np.zeros(img.shape)

for (i,ch) in enumerate(['R','G','B']):
    mean_convolved[:,:,i] = convolve2d_1ch(img[:,:,i], kernel, padding='edge')
    
mean_convolved = mean_convolved.astype('uint8')

img_show2(img, mean_convolved)

平均化フィルタによる平滑化の結果, ブラーがかかっていることがわかります。

3.1.2 opencvによる実装

　OpenCVでは, cv2.filter2D 関数を用いることで任意カーネルによる畳み込みができ, cv2.blur 関数を用いることで平均化フィルタを利用できるようです。

img = cv2.cvtColor(cv2.imread('img_src/wizdomiot.png',1), cv2.COLOR_BGR2RGB)

blur = cv2.blur(img,(29,29))

img_show2(img, blur)

手実装したものと速度比較してみます。

%%timeit
blur = cv2.blur(img,(29,29))

3.55 ms ± 235 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)

%%timeit
N = 29
kernel = np.ones([N,N]) / (N*N)
mean_convolved = np.zeros(img.shape)
for (i,ch) in enumerate(['R','G','B']):
    mean_convolved[:,:,i] = convolve2d_1ch(img[:,:,i], kernel, padding='edge')
mean_convolved = mean_convolved.astype('uint8')

4.07 s ± 507 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)

N=29 で 1000 倍ほどの速度差が出ました。OpenCVはすごいですね。

また, N=5 などの小さい数で比較してみると,

%%timeit
blur = cv2.blur(img,(5,5))

2.68 ms ± 300 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)

%%timeit
N = 5
kernel = np.ones([N,N]) / (N*N)
mean_convolved = np.zeros(img.shape)
for (i,ch) in enumerate(['R','G','B']):
    mean_convolved[:,:,i] = convolve2d_1ch(img[:,:,i], kernel, padding='edge')
mean_convolved = mean_convolved.astype('uint8')

284 ms ± 6 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)

　このように, OpenCVでは N=5 と N=29 で速度差があまりない一方で, 畳み込み演算を素朴に実装した方は N に比例して大きくなってしまっていることがわかります。

畳み込み演算の計算を考えると, こちらの時間計算量は $O(N^2)$ といったところでしょうか。

3.2. ガウシアンフィルタ

　平均化フィルタでは, 目的のピクセルとその周辺のピクセルを同じ重みづけで計算をしていたことになりますが, 目的のピクセルに近いピクセルの比重を大きくすることも考えられます。

　そこで, 目的のピクセルを中心とした ガウス分布(正規分布) に従って重み付き平均を計算するフィルタのことを, ガウシアンフィルタ と呼びます。

　今回使うカーネルは二次元なので, 以下のような二次元ガウス分布になります。

平均:0, 分散: $ σ^2$ の二次元正規分布:
$ h_g(x,y) = \dfrac{1}{2 \pi σ^{2}} \exp \bigg( - \dfrac{ x^{2}+y^{2}}{2 σ^{2} } \bigg) $

とりあえずこれをそのまま関数化して,

# 平均 0, 分散 sigma^2 の二次元ガウス分布
def norm2d(x,y,sigma):
    Z = np.exp(-(x**2 + y**2) / (2 * sigma**2)) / (2 * np.pi * sigma**2)
    return Z

プロットしてみると,

sns.set_style('ticks')

fig = plt.figure(figsize=(10,8))
ax = fig.add_subplot(111, projection='3d')

x = y = np.arange(-3,3,0.1)
X,Y = np.meshgrid(x,y)

ax.plot_surface(X,Y,norm2d(X,Y,1),cmap='coolwarm')
plt.show()

このような感じです。二次元になっただけの普通の正規分布です。

これを平均化カーネルの重み付けに利用するのですが,

「フィルタサイズ (2w + 1)(2w + 1) の場合，σ = w/2 とするのが一つの目安」 http://www.clg.niigata-u.ac.jp/~lee/jyugyou/img_processing/medical_image_processing_03_press.pdf

というような記述があったので, ひとまずこれに従ってみることにします。

以上を踏まえて, ガウシアンフィルタのためのカーネル行列を作成する関数を以下に実装しました。

def gaussian_kernel(size):
    if size%2==0:
        print('kernel size should be odd')
        return
    sigma = (size-1)/2
    
    # [0,size]→[-sigma, sigma] にずらす
    x = y = np.arange(0,size) - sigma
    X,Y = np.meshgrid(x,y) 
    
    mat = norm2d(X,Y,sigma)
    
    # 総和が1になるように
    kernel = mat / np.sum(mat)
    return kernel

以下のようになります。

gaussian_kernel(3)

array([[ 0.07511361,  0.1238414 ,  0.07511361],
       [ 0.1238414 ,  0.20417996,  0.1238414 ],
       [ 0.07511361,  0.1238414 ,  0.07511361]])

gaussian_kernel(5)

array([[ 0.02324684,  0.03382395,  0.03832756,  0.03382395,  0.02324684],
       [ 0.03382395,  0.04921356,  0.05576627,  0.04921356,  0.03382395],
       [ 0.03832756,  0.05576627,  0.06319146,  0.05576627,  0.03832756],
       [ 0.03382395,  0.04921356,  0.05576627,  0.04921356,  0.03382395],
       [ 0.02324684,  0.03382395,  0.03832756,  0.03382395,  0.02324684]])

中央が一番大きく, 周辺に向かうにつれて割合が減衰していることがわかると思います。

カーネルが用意できたので, 早速畳み込んでみましょう。

gauss_convolved = np.zeros(img.shape)

for (i,ch) in enumerate(['R','G','B']):
    gauss_convolved[:,:,i] = convolve2d_1ch(img[:,:,i], gaussian_kernel(29), padding='edge')
    
gauss_convolved = gauss_convolved.astype('uint8')

img_show2(img, gauss_convolved)

かかりました。先ほどの平均化フィルタとの違いがよくわからないので, 並べてみます。

img_show2(mean_convolved, gauss_convolved,['mean','gaussian'])

やや微妙な差ですが, ガウシアンフィルタのほうがなめらかな結果になっています。

3.3. 応用 : 特定方向の平滑化

　上記の応用として, 特定方向のみの平滑化, いわゆるブラー(方向)があります。これは, 特定方向のみの平均を取ることによって実現できます。

# 5*5 単位行列を5で割る
np.eye(5)/5

array([[ 0.2,  0. ,  0. ,  0. ,  0. ],
       [ 0. ,  0.2,  0. ,  0. ,  0. ],
       [ 0. ,  0. ,  0.2,  0. ,  0. ],
       [ 0. ,  0. ,  0. ,  0.2,  0. ],
       [ 0. ,  0. ,  0. ,  0. ,  0.2]])

例えば, 上記のようなカーネルを用いることで, 斜め方向の平滑化が可能になります。

N=39
kernel = np.eye(N)/N

convolved_1 = np.zeros(img.shape)

for (i,ch) in enumerate(['R','G','B']):
    convolved_1[:,:,i] = convolve2d_1ch(img[:,:,i], kernel, padding='edge')
    
convolved_1 = convolved_1.astype('uint8')

img_show2(img, convolved_1)

斜めにかかりました。しかし, あまり仕上がりが綺麗ではありません。

そこで, 先ほどと同じように, 正規分布に従って重み付けをしてみることにします。シンプルに以下のようにします。

mat = gaussian_kernel(5)*np.eye(5)
mat / np.sum(mat)

array([[ 0.11170336,  0.        ,  0.        ,  0.        ,  0.        ],
       [ 0.        ,  0.23647602,  0.        ,  0.        ,  0.        ],
       [ 0.        ,  0.        ,  0.30364122,  0.        ,  0.        ],
       [ 0.        ,  0.        ,  0.        ,  0.23647602,  0.        ],
       [ 0.        ,  0.        ,  0.        ,  0.        ,  0.11170336]])

N=39
mat = gaussian_kernel(N)*np.eye(N)
kernel = mat / np.sum(mat)

convolved_2 = np.zeros(img.shape)

for (i,ch) in enumerate(['R','G','B']):
    convolved_2[:,:,i] = convolve2d_1ch(img[:,:,i], kernel, padding='edge')
    
convolved_2 = convolved_2.astype('uint8')

img_show2(img, convolved_2)

img_show2(convolved_1,convolved_2,['mean','gaussian'])

これは右のガウス分布重み付き平均のほうが綺麗だと思うのですが, いかがでしょうか。。。

ここで, 任意方向の平滑化を作ってみたいと思います。カーネルの作り方は色々ありえると思いますが, ここでは cv2.line() 関数を用いてみます。

具体的には, cv2.line() では, 始点と終点の座標を指定することで以下のように「線を引く」ことができるので,

N=7
bg = np.zeros([N,N])
bg_lined = cv2.line(bg,(2,0),(4,7),1,1)
print(bg_lined)

[[ 0.  0.  1.  0.  0.  0.  0.]
 [ 0.  0.  1.  0.  0.  0.  0.]
 [ 0.  0.  0.  1.  0.  0.  0.]
 [ 0.  0.  0.  1.  0.  0.  0.]
 [ 0.  0.  0.  1.  0.  0.  0.]
 [ 0.  0.  0.  0.  1.  0.  0.]
 [ 0.  0.  0.  0.  1.  0.  0.]]

これを重み付き平均の係数の形にしてあげればよい,ということです。

gauss_lined = bg_lined * gaussian_kernel(N)
kernel = gauss_lined / np.sum(gauss_lined)
print(kernel)

[[ 0.          0.          0.10329792  0.          0.          0.          0.        ]
 [ 0.          0.          0.13637317  0.          0.          0.          0.        ]
 [ 0.          0.          0.          0.17030948  0.          0.          0.        ]
 [ 0.          0.          0.          0.18003887  0.          0.          0.        ]
 [ 0.          0.          0.          0.17030948  0.          0.          0.        ]
 [ 0.          0.          0.          0.          0.13637317  0.          0.        ]
 [ 0.          0.          0.          0.          0.10329792  0.          0.        ]]

これを, 任意の角度の入力に対して行えるようにしたカーネル作成関数を実装します。

始点と終点の座標は行列の外側でもかまわないことに注意すると, 以下のようになるかと思います。

def directional_kernel(size,angle):
    if size%2==0:
        print('kernel size should be odd')
        return
    
    angle = angle % 180
    radian = (angle/180) * np.pi
    
    x1 = int(np.cos(radian)*(size/2) + (size/2))
    y1 = int(np.sin(radian)*(size/2) + (size/2))
    x2 = int(np.cos(radian + np.pi)*(size/2) + (size/2))
    y2 = int(np.sin(radian + np.pi)*(size/2) + (size/2))
    
    bg = np.zeros([size,size])
    bg_lined = cv2.line(bg,(x1,y1),(x2,y2),1,1)
    gauss_lined = bg_lined * gaussian_kernel(size)
    kernel = gauss_lined / np.sum(gauss_lined)
    return kernel

実行してみます。

directional_kernel(5,0)

array([[ 0.        ,  0.        ,  0.        ,  0.        ,  0.        ],
       [ 0.        ,  0.        ,  0.        ,  0.        ,  0.        ],
       [ 0.15246914,  0.2218413 ,  0.25137912,  0.2218413 ,  0.15246914],
       [ 0.        ,  0.        ,  0.        ,  0.        ,  0.        ],
       [ 0.        ,  0.        ,  0.        ,  0.        ,  0.        ]])

directional_kernel(5,30)

array([[ 0.        ,  0.        ,  0.        ,  0.        ,  0.        ],
       [ 0.14343172,  0.20869192,  0.        ,  0.        ,  0.        ],
       [ 0.        ,  0.        ,  0.26796573,  0.23647892,  0.        ],
       [ 0.        ,  0.        ,  0.        ,  0.        ,  0.14343172],
       [ 0.        ,  0.        ,  0.        ,  0.        ,  0.        ]])

directional_kernel(5,60)

array([[ 0.        ,  0.14343172,  0.        ,  0.        ,  0.        ],
       [ 0.        ,  0.20869192,  0.        ,  0.        ,  0.        ],
       [ 0.        ,  0.        ,  0.26796573,  0.        ,  0.        ],
       [ 0.        ,  0.        ,  0.23647892,  0.        ,  0.        ],
       [ 0.        ,  0.        ,  0.        ,  0.14343172,  0.        ]])

このような形になりました。実際に使ってみると,

def directinal_blur(img, N, angle):
    convolved = np.zeros(img.shape)
    
    for (i,ch) in enumerate(['R','G','B']):
        convolved[:,:,i] = convolve2d_1ch(img[:,:,i], directional_kernel(N,angle), padding='edge')
    convolved = convolved.astype('uint8')
    
    img_show2(img, convolved)

directinal_blur(img,N=39,angle=0)

directinal_blur(img,N=39,angle=30)

directinal_blur(img,N=39,angle=60)

directinal_blur(img,N=39,angle=90)

0,30,60,90度の方向にブラーがかかっていることがわかります。

4. おわりに

　今回は, 畳み込みといくつかの平滑化フィルタを実装することで, 空間フィルタリングに関する初歩的な理解を得ることができました。

　次回は, メディアンなどのエッジを保存する平滑化フィルタについて扱おうかと思います。

5. 参考文献

• 「ディジタル画像処理」の6章

• http://www.clg.niigata-u.ac.jp/~lee/jyugyou/img_processing/medical_image_processing_03_press.pdf

• numpyのas_stridedはどのように使うのか

• python - Convolve2d just by using Numpy - Stack Overflow

• 画像の平滑化 — OpenCV-Python Tutorials 1 documentation