Python3 & OpenCV で画像処理を学ぶ[4] 〜 アルファブレンドとエンボス効果(画像間演算の基礎)
1. はじめに
前回は、一つの画像の画素値に対して個々に変換を行うトーンカーブについて学びました。
今回は、二つの画像の画素値を受け取って変換を行い、一つの画素値として返す処理を学びます。具体的には、画像の上に画像を重ねた時の処理についてです。
その代表的な例として、アルファブレンディングやエンボス効果などについてまとめ、実装を行ってみたいと思います。
import numpy as np from matplotlib import pyplot as plt from mpl_toolkits.mplot3d import Axes3D import seaborn as sns import cv2 %config InlineBackend.figure_format = 'retina'
2. 画像ブレンドの基礎
2.1. 画像間演算
二枚(以上)の画像が与えられたとき、同じ位置にある各画像の画素値に対して何らかの演算を行い、一つの画素値として出力することを画像間演算と呼びます。そのような処理にはどのようなものがあるでしょうか。
画面上重なる位置にある(=入力される)2つの画素の値を $x, y$と、 出力される画素値を $z$ とおきます。シンプルな例では、
加算
$z = x + y$乗算
$z = xy$単純平均
$z = \dfrac{x + y}{2}$
などがありえそうです。
「$x,y$ の二つの入力が与えられることで、 $z$ の値が一通りに決まる」関係ということになるので、二変数関数 $z=f(x,y)$ として考えられそうです。
以下、より具体的に見ていくことにします。
2.2. アルファブレンディング
(R,G,B) の3つのチャンネルの他、不透明度を示すアルファ値 A を加えて (R, G, B, A)とすることがあり、Photoshopなどのレイヤー構造を持つソフトウェアでは、アルファ値によって下のレイヤーが透けたりすることは周知だと思います。
アルファ値による透過に見えるこの処理(アルファブレンディング)が、画像間演算としてはどのようなものになるのかを見ていくことにします。
以下では簡単のため、RGB値とアルファ値はすべて 0 と 1 の間の実数として考えます。単に255で割れば[0,255]と対応します。
$ 0 \leq {RGB} \leq 1$
$0 \leq \alpha \leq 1 $
そして、入出力の画素のRGB値, アルファの値を以下のように書くことにします。
前景(上のレイヤー): ${RGB}_1$, $\alpha_1$
背景(下のレイヤー): ${RGB}_2$, $\alpha_2$
出力(演算結果) : ${RGB}$, $\alpha$
2.2.1 $\alpha_2=1$ と仮定する場合
下のレイヤーの画素が完全に不透明($\alpha_2=1$)なときの式は、以下のようになります。
下のレイヤーが完全に不透明なため、上にどんな不透明度の画素が乗っても当然出力は $\alpha=1$ です。
また、RGB値については、幾何的に${RGB}_1,{RGB}_2$をRGB空間中の二点と考えたとき、それらを $\alpha_1 : (1-\alpha_1)$ で内分した点が $ {RGB} $ になると考える事ができます。
以下の図のようなイメージです。
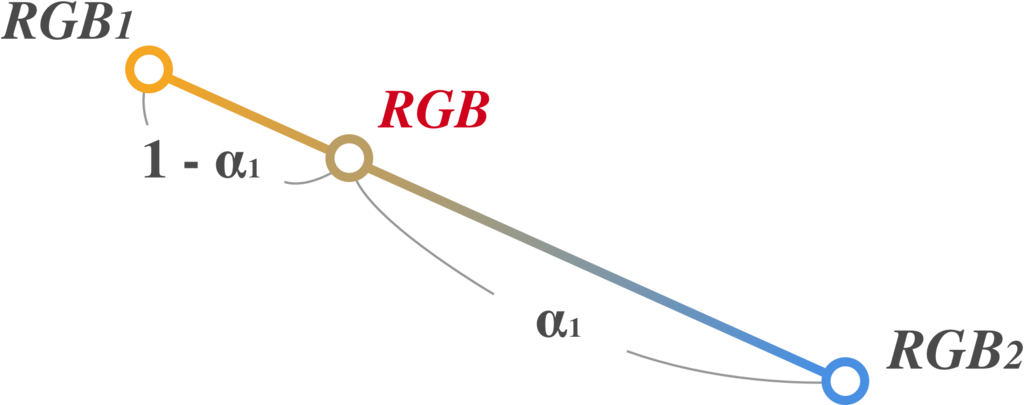
つまり、上のレイヤーの不透明度 $\alpha_1$ が大きければ、出力が上のレイヤーの ${RGB}_1$ に近くなり、逆に$\alpha_1$ が小さければ、${RGB}_2$ に近くなるということですね。
この演算によって、「上のレイヤーが透けている」ような見え方が実現できている、ということです。
2.2.2 $\alpha_2=1$ とは限らない一般の場合
次に、下のレイヤーが半透明($\alpha_2\neq1$)なときの式は、以下のようになります。
(ただし, $\alpha=0$ つまり出力画素が完全な透明のときは ${RGB}=0$ とする.)
ここで、
$\alpha = \ \alpha_1 + \alpha_2 (1 - \alpha_1)$
の式を理解するために、この式を
$z = x + y (1 - x)$
という二変数関数であるとみなして、三次元作図をしてみることにします。
# jupyterで三次元プロットを動的に動かすには、以下のマジックコマンドでグラフを外部出力する必要あり %matplotlib N= 20 x = np.linspace(0, 1, N) y = np.linspace(0, 1, N) X,Y = np.meshgrid(x,y) P = np.c_[np.ravel(X), np.ravel(Y)] def alpha(A): Z = A[0] + A[1] * (1-A[0]) return Z Z = np.apply_along_axis(alpha, 1, P).reshape(X.shape) sns.set_style('ticks') fig = plt.figure() ax = fig.add_subplot(111,projection='3d') surf = ax.plot_surface(X,Y,Z,cmap='binary',linewidth=4) ax.set_xlabel('foreground alpha') ax.set_ylabel('background alpha') ax.set_zlabel('blended') plt.show()
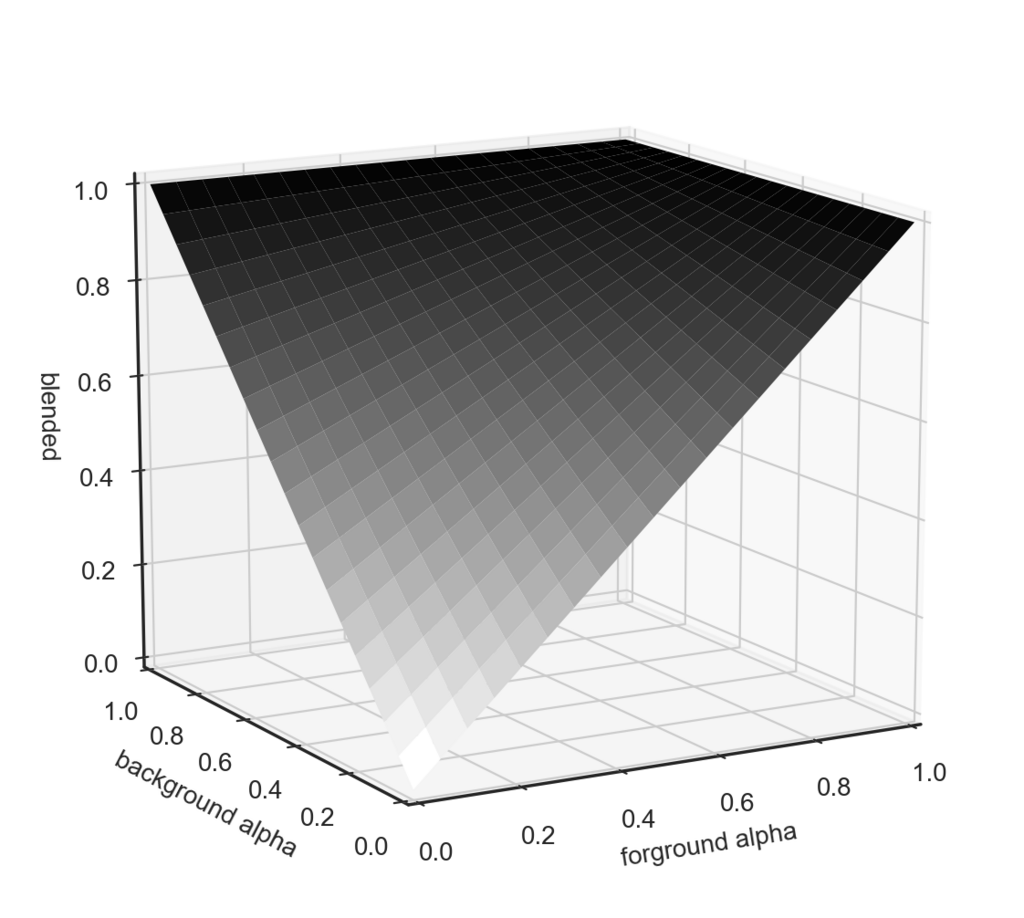
すると、以上のようになりました。
左奥方向が背景のアルファ値$\alpha_2$、右方向が前景のアルファ値$\alpha_1$、上方向がブレンドした結果の$\alpha$ です。
こうしてみると、 $\alpha = \ \alpha_1 + \alpha_2 (1 - \alpha_1)$ という式は、「半透明な2枚の層の重ね合わせ」に対して自然に要請される性質、すなわち「常に$max(\alpha_1,\alpha_2)\leq \alpha$ を満たし(合成で減らない)」、かつ「少なくとも$\alpha_1,\alpha_2$のどちらか一方が $1$ でない限り結果も$\alpha=1$にならない」という条件を満たすような演算であることが視覚的にわかります。
2.2.3 プリマルチプライド
ところで、先ほどの式
のRGBの行では、${RGB}_1 \alpha_1 + {RGB}_2 \alpha_2$ というようにRGB値にその画素のアルファ値を乗算しています(→透明な部分が暗くなる)。
これをアルファブレンドの際に行わなくて良いように、あらかじめ画像のRGB値をアルファ値を乗算したものにしておくという方式があります(乗算済みアルファ、プリマルチプライド)。
そのようにした場合、アルファブレンドの計算式は以下のようになります。
かなり式が簡潔になりました。合成のたびにアルファ値を乗算したり割ったりする手間が省けるため、計算の高速化が見込めそうです。
2.2.4 アルファブレンド実装実験
理論的な話が多くなったので、ここで手を動かす事にします。上記の式を元に、アルファブレンドを実装をしてみます。
以下は、それぞれ下半分・右半分にマスクを書けた二枚の画像をプリマルチプライしたのち、ブレンドを行うコードです。
%matplotlib inline """ 二枚の画像のアルファ値を調整し下半分・右半分をマスキング。 プリマルチプライしたのちにアルファブレンドを実行して表示。 """ # imread(path,-1)でBGRAとして読み込み. ともに(720, 1280, 4)の配列 pdr = cv2.cvtColor(cv2.imread('img_src/pandra.png',-1),cv2.COLOR_BGRA2RGBA) sb = cv2.cvtColor(cv2.imread('img_src/SCARY BANQUET1.png',-1),cv2.COLOR_BGRA2RGBA) # [0,1] に正規化 pdr = pdr / 255 sb = sb / 255 y = pdr.shape[0] x = pdr.shape[1] # やや強引だが、pdrを画面の上1/3から2/3にかけてα=1→0となるようにする。sbは左から右で # pdrを背景, sbを前景にする想定 pdr[:,:,3] = np.linspace(1.5,-0.5,y).repeat(x).reshape(y,x).clip(0,1) sb[:,:,3] = np.linspace(1.5,-0.5,x).repeat(y).reshape(x,y).T.clip(0,1) # Premultiply(今回は一回だけの合成なのであまり意味がないが) for (i,ch) in enumerate(['R','G','B']): pdr[:,:,i] = pdr[:,:,i] * pdr[:,:,3] sb[:,:,i] = sb[:,:,i] * sb[:,:,3] blended = np.zeros(pdr.shape) # alphaの式 blended[:,:,3] = sb[:,:,3] + pdr[:,:,3] * (1 - sb[:,:,3]) # RGBの式 for (i,ch) in enumerate(['R','G','B']): blended[:,:,i] = sb[:,:,i] + pdr[:,:,i] * (1 - sb[:,:,3]) gs = gridspec.GridSpec(3,2) fig = plt.figure(figsize=(10,9)) ax1 = fig.add_subplot(gs[0,0]) ax2 = fig.add_subplot(gs[0,1]) ax3 = fig.add_subplot(gs[1:3,:]) ax1.set_xticks([]), ax1.set_yticks([]) ax2.set_xticks([]), ax2.set_yticks([]) # アルファは無視して表示 ax1.set_title('Background') ax1.imshow(pdr[:,:,:3]) ax2.set_title('Foreground') ax2.imshow(sb[:,:,:3]) ax3.set_title('Blended') ax3.imshow(blended[:,:,:3]) plt.show()

以上のようになりました。コードの通り、上に表示された画像自体はアルファチャンネルを持っていません。
つまり、不透明度はアルファ値によって直接表現されているわけではなく、アルファ値をRGB値に乗算することによって表現されるということです。
次に、上の画像のプリマルチプライドを解除してみます。つまり、RGB値をアルファ値で割ります。
# プリマルチプライドの解除つまり除算をするので、ゼロ除算回避用のマスク mask = blended[:,:,3]!=0 upmply = np.zeros(blended.shape) for (i,ch) in enumerate(['R','G','B']): upmply[mask,i] = blended[mask,i] / blended[mask,3] upmply = (upmply*255).astype('uint8') plt.figure(figsize=(16,9)) plt.title('un-premultiplied') plt.imshow(upmply[:,:,:3]) plt.show()

以上のようになりました。上の画像(本来のRGB値)にアルファ値が乗算されることで、半透明に見えていたというわけですね。
また、二枚の画像が重なる部分では、先ほど説明した「${RGB}_1,{RGB}_2$ を $\alpha_1 : (1-\alpha_1)$ で内分した点が $ {RGB} $ になる」という事の意味を視覚的に確かめることができます。
次に、アルファ値の計算式の確認として、 α=1 となるピクセルのみを表示することにしてみます。
partialy_opac = blended[:,:,3]!=1 opac = blended for (i,ch) in enumerate(['R','G','B']): opac[partialy_opac,i] = blended[partialy_opac,i] * 0 opac = (opac*255).astype('uint8') plt.figure(figsize=(16,9)) plt.title('only α=1 pixels') plt.imshow(opac[:,:,:3]) plt.show()

以上のようになりました。二枚の画像のどちらか一方がα=1となる領域だけが残ることがわかります。
この結果から、「少なくとも$\alpha_1,\alpha_2$のどちらか一方が $1$ でない限り結果も$\alpha=1$にならない」という事実を確かめることができました。
2.2.5 アルファブレンドのまとめ
結論として、アルファ値というのは見かけ上「不透明度」であり、そのように捉えてほぼ問題ないのですが、計算上はあくまで「画像間演算の際、それぞれのRGB値に対して乗算される係数」に過ぎず、不透明度をそれ自身で直接表現しているものではないということです。
以上のことを原理的に理解すれば、例えば「不透明度50%のレイヤーを二枚重ねても不透明度100%にならない」などの個別具体的な現象の意味も了解できるかと思います。
2.3. エンボス効果
次はエンボス効果です。こちらはアルファブレンドに比べると話題としてはややおまけ程度なのですが、画像間演算を別の側面から眺める例として。
画像を浮き上がったように見せるエンボス効果は、以下の手続きで実現する事ができます。
「ある元画像 $A$ と、$A$の明度を反転して少し斜めに移動した$A'$を加算合成し、$0.5$を引く。ただし、$0$を下回ったり$1$を超えた値は、$[0,1]$の範囲にクリップする」
早速、具体的に実装していきたいと思います。 まずは元画像です。
# グレースケールにしておく img = cv2.cvtColor(cv2.imread('img_src/lyrith.png',0),cv2.COLOR_GRAY2RGB) img = img / 255 plt.figure(figsize=(16,9)) plt.imshow(img) plt.show()

次に、この画像の明度を反転します。前回の記事のように、シンプルに階調変換関数を作って適用することにします。
def invert(pixel): return 1 - pixel img_2 = np.array([invert(a) for a in img]) plt.figure(figsize=(16,9)) plt.imshow(img_2) plt.show()

反転できました。
次は斜めへの移動です。
あるピクセルの座標 $\mathbf{P} = \left( \begin{array}{c} p_x \\ p_y \\ \end{array} \right)$ を、 $ \left( \begin{array}{c} x \\ y \\ \end{array} \right)$方向へ $ \left( \begin{array}{c} \Delta x \\ \Delta y \\ \end{array} \right)$ だけ移動させるには、以下の変換行列 $\mathbf{T}$ を用います。
すなわち、$\mathbf{P}$ に 変換行列 $\mathbf{T}$ を左からかけることで、移動後の座標$\mathbf{P'}$ を
として、得ます。
OpenCVでこれを行うには、cv2.warpAffine(img, Matrix,(colnum,rownum)) 関数を用います。
第二引数のMatrixに、変換行列をfloat32のnumpy配列として与えることで、変換後の画像を得ることができます。
# 移動量 dx = -5 dy = -5 # 変換行列 M = np.float32([[1,0,dx],[0,1,dy]]) rownum,colnum = img_2.shape[:2] plt.figure(figsize=(16,9)) img_2 = cv2.warpAffine(img_2, M,(colnum,rownum)) # (列数, 行数)の順であることに注意 plt.imshow(img_2) plt.show()

平行移動ができました。(移動が微小なのでわかりにくいですが、右下を見ると少しずれています)
最後に、これと元画像を重ねて $0.5$ を引きます。
add = img + img_2 emboss = add - 1/2 emboss = emboss.clip(0,1) plt.figure(figsize=(16,9)) plt.imshow(emboss) plt.show()

エンボス効果ができました。リリスだと映えますね。
このような処理でエンボス効果になる仕組みは、以下の図のようなイメージです。
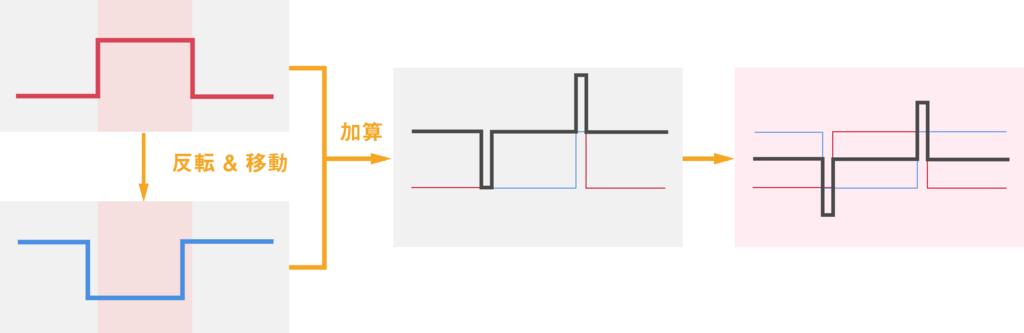
元画像とそれを反転した画像を単に加算合成すると何も見えなくなりますが、少しの平行移動によって凹凸だけが残るようになる、という感じですね。
3. おわりに
今回は、アルファブレンドとエンボス効果について学びながら実装することを通して、画像ブレンド(画像間演算)の基礎を理解することができました。
次回↓は、(やや寄り道気味ですが、)Photoshopなどにある描画モードを一通り実装します。